本学点是高考考查的热点之一,也是本章内容的学习重点.仅就基本概念和简单性质的考查而言,命题类型多为灵活多变的选择题或填空题,一般说来求解此类小题难度不大.
有关数列的试题经常把数列知识和指数函数、对数函数及不等式的知识综合起来.探索性问题是高考的热点,常在数列解答题中出现.
例1.(2005年全国I高考试题)设等比数列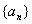 的公比为q,前n项和Sn>0(n=1,2,…)
的公比为q,前n项和Sn>0(n=1,2,…)
(1)求q的取值范围;
(2)设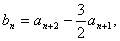 记
记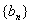 的前n项和为Tn,试比较Sn和Tn的大小.
的前n项和为Tn,试比较Sn和Tn的大小.
本小题主要考查等比数列的基本知识,考查分析问题能力和推理能力,满分12分.
解:(Ⅰ)因为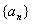 是等比数列,
是等比数列,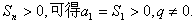
当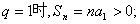
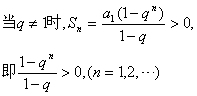
上式等价于不等式组: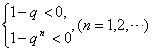 ①
①
或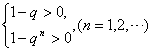 ②
②
解①式得q>1;解②,由于n可为奇数、可为偶数,得-1<q<1.
综上,q的取值范围是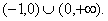
(Ⅱ)由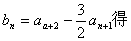
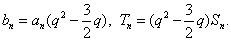
于是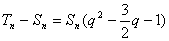
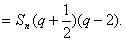

例2.(2003年天津高考试题)设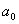 为常数,且
为常数,且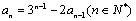
(1)证明对任意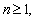
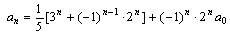 ;
;
(2)假设对任意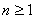 有
有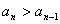 ,求
,求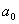 的取值范围.
的取值范围.
解答:(1)证法一:(i)当n=1时,由已知a1=1-2a0,等式成立;
(ii)假设当n=k(k≥1)等式成立,则
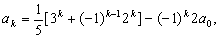
那么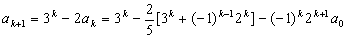
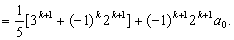
也就是说,当n=k+1时,等式也成立.根据(i)和(ii),可知等式对任何n∈N且n≥1成立.
证法二:如果设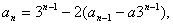 用
用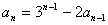 代入,可解出
代入,可解出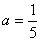 .
.
所以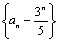 是公比为-2,首项为
是公比为-2,首项为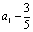 的等比数列.
的等比数列.
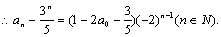
即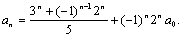
(2)解法一:由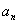 通项公式
通项公式
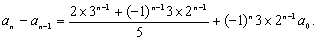
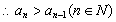 等价于
等价于
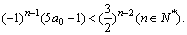 ……①
……①
(i)当n=2k-1,k=1,2,…时,①式即为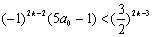
即为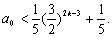 ……②
……②
②式对k=1,2,…都成立,有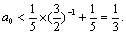
(ii)当n=2k,k=1,2,…时,
①式即为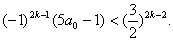
即为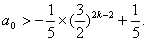 …… ③
…… ③
③式对k=1,2,…都成立,有
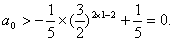
综上,①式对任意n∈N*,成立,有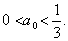
故a0的取值范围为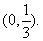
解法二:如果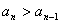 (n∈N*)成立,特别取n=1,2有
(n∈N*)成立,特别取n=1,2有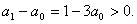
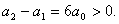 因此
因此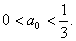 下面证明当
下面证明当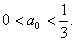 时,对任意n∈N*,
时,对任意n∈N*,
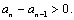 由an的通项公式
由an的通项公式
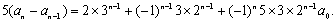
(i)当n=2k-1,k=1,2,…时,
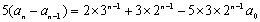
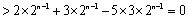
(ii)当n=2k,k=1,2…时,
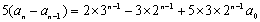
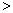
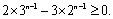
故a0的取值范围为