例:有以下真命题:设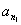 ,
,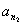 ,…,
,…,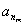 是公差为
是公差为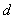 的等差数列
的等差数列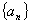 中的任意
中的任意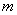 个项,
个项,
若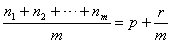 (
(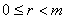 ,
,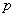 、
、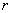 、
、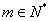 或
或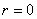 ) ①,
) ①,
则有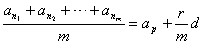 ②,
②,
特别地,当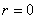 时,称
时,称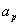 为
为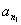 ,
,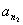 ,…,
,…,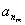 的等差平均项.
的等差平均项.
(1)当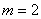 ,
,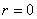 时,试写出与上述命题中的①,②两式相对应的等式;
时,试写出与上述命题中的①,②两式相对应的等式;
(2)已知等差数列 的通项公式为
的通项公式为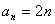 ,试根据上述命题求
,试根据上述命题求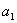 ,
,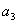 ,
,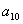 ,
,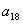 的等差平均项;
的等差平均项;
(3)若数列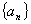 为等差数列,
为等差数列,
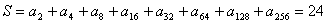 ,且
,且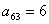 ,求该数列的通项公式.
,求该数列的通项公式.
(4)试将上述真命题推广到各项为正实数的等比数列中,写出相应的真命题(不要求证明).
解答:(1)若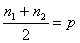 ,则
,则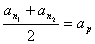 .
.
(2)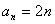 ,
,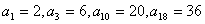 .
.
∵ 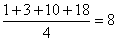 ,∴
,∴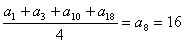 .
.
(3)∵ 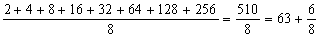 ,
,
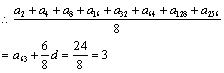
∵ 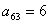 ,∴
,∴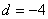 ,
,
∴ 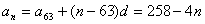 .
.
(4)有以下真命题:设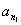 ,
,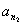 ,…,
,…,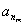 是公比为
是公比为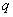 的等比数列
的等比数列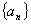 中的任意
中的任意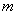 个项,
个项,
若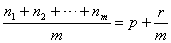 (
(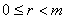 ,
,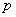 、
、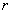 、
、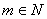 或
或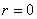 ) ①,
) ①,
则有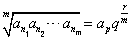 ②,
②,
特别地,当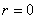 时,称
时,称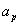 为
为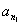 ,
,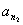 ,…,
,…,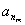 的等比平均项.
的等比平均项.