主讲： 教师　李新潮

一周强化

一、一周知识概述

1、三角函数的图象

2、三角函数的性质

　　（1）正弦函数的性质——y=sinx的定义域是R，值域是[－1，1]，奇函数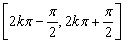，在上递增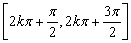，在上递减，在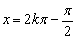时，取最小值－1，在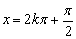时，取最大值1（其中k∈Z）.

　　（2）余弦函数的性质——y=cosx的定义域是R，值域是[－1，1]，偶函数，在[2kπ，2kπ＋π]上递减，在[2kπ＋π，2kπ＋2π]上递增，在x=2kπ时取最大值1，在x=2kπ＋π时取最小值－1（其中K∈Z）.

　　（3）正切函数的性质——y=tgx的定义域是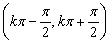，值域是R，奇函数，在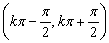上递增，没有最大、最小值（其中k∈Z）.

　　（4）三角函数的周期

　　①周期函数——对于函数y=f(x)，如果存在一个不为零的常数T，使得当x取定义域内的每一个值时，f(x＋T)=f(x)都成立，那么就把函数y=f(x)叫做周期函数，不为零的常数T叫做这个函数的周期.

　　②最小正周期——对于一个周期函数来说，如果在所有的周期中存在着一个最小的正数，就把这个最小的正数叫做最小的正周期.

　　③三角函数的最小正周期——y=sinx和y=cosx的最小正周期T=2π，y=tgx和y=ctgx的最小正周期T=π.

3、函数y=sinx与y=Asin(ωx＋Φ)，(A＞0，Φ＞0)的比较.

二、重、难点知识的归纳与剖析

1、本周学习的重点

（1）三角函数不等式的解法与三角函数单调区间的求法.

（2）三角函数的最值问题.

（3）三角函数的图象与性质的运用.

（4）周期性、对称性在解题中的应用.

2、本周学习的难点

（1）正确、有效地运用三角函数的图象解决问题.

（2）已知三角函数值求角.

（3）对符号“arcsina”、“arccosa”、“arctana”的正确理解，及正确运用这三个符号表示角.

（4）三角函数的图象变换.

三、例题点评

例1、用五点法作出函数的图象，并说明它与y=sinx的图像间的变换关系.

[解析]

例2、（1）求函数的定义域、值域；

　　 （2）求函数的值域.

[解析]

例3、求下列函数的单调递减区间.

　　

[解析]

例4、 已知函数f(x)=1－2a－2acosx－2sin2x的最小值为g(a)，a∈R.

（1）求g(a)；

（2）若，求a及此时f(x)的最大值.

[解析]

例5、 已知y=f(x)是定义在R上的函数，且对任意x∈R，有f(x＋2)[1－f(x)]=f(x)＋1成立.

　（1）证明y=f(x)是周期函数；

　（2）若f(1)=－2，求f(2005)的值.

[解析]