|
一周强化
一、一周知识概述
本节内容是在上一节解三角形的基础上提出了更高的要求,要我们能从实际问题中抽象出一个或几个三角形.并根据已知条件分析出这些三角形中的对应量,再运用所学的解三角形的知识去解决问题,从而达到提高解决实际问题的能力.
二、知识归纳及讲解
1、解斜三角形应用题的一般步骤是:
①分析:理解题意,分清已知与未知,画出示意图,抽象成三角形相应边和角及相应大小、位置,从而成为一个纯解三角形的问题.
②建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学模型.
③求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解.
④检验:检验上述所求的解是否符合实际意义,从而得出实际问题的结论.
解斜三角的基本思路
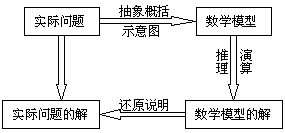
2、常用术语与相关概念
(1)坡度(亦叫坡角):坡与水平面的夹角的度数.
(2)坡比:坡面的铅直高度与水平宽度之比,即坡角的正切值.
(3)仰角和俯角:与目标视线在同一铅直平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫仰角,目标视线在水平视线下方时叫俯角.
(4)方向角:从指定方向线到目标方向线的水平角.
(5)方位角:从指北方向线顺时针到目标方向线的水平角.
三、难点知识剖析
1、解斜三角形应用题的一般步骤是:
(1)分析:理解题意,分清已知与未知,画出示意图.
(2)建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学模型.
(3)求解:利用正弦定理或余弦定理有序地解出三角形,求出数学模型的解.
(4)检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解.
2、解斜三角形应用题常见的几种情况:
(1)实际问题经抽象概括后,已知与未知量全部集中在一个三角形中,一次可用正弦定理或余弦定理解之.
(2)实际问题经抽象概括后,已知量与未知量涉及两个三角形中,这时需按顺序逐步在两个三角形中求出问题的解.
(3)实际问题经抽象概括后,涉及的三角形只有一个,但由题目已知条件解此三角形需连续使用正弦定理或余弦定理.
四、例题讲解
例1、如图,为了测定河的宽度,在河岸取定基线BC,其长为α,在河对岸取定点A,测得∠ABC=α,∠ACB=β,求河宽.
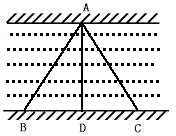
[分析与解答]
例2、隔河看两目标A与B,但不能到达,在岸边选取相距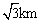 的C、D两点,同时,测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内).求两目标A、B之间的距离. 的C、D两点,同时,测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内).求两目标A、B之间的距离.
[分析与解答]
例3、在海岸A处,发现北偏东45°方向,距A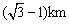 的B处有一艘走私船.在A处北偏西75°方向,距A为 的B处有一艘走私船.在A处北偏西75°方向,距A为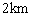 的C处的缉私船奉命以 的C处的缉私船奉命以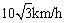 的速度追截走私船,此时走私船正以10km/h 的速度从B处向北偏东30°方向逃窜.问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. 的速度追截走私船,此时走私船正以10km/h 的速度从B处向北偏东30°方向逃窜.问缉私船沿什么方向能最快追上走私船,并求出所需要的时间.
[分析与解答]
例4、如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100m后,又从B点测得斜度为45°,设建筑物的高为50m.求此山对于地平面的斜度的倾斜角θ(用反三角函数表示).
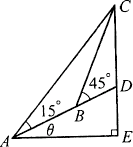
[分析与解答]
例5、A、B、C是一条直路上的三点,AB=BC=1km,从这三点分别遥望一座电视发射塔P,A见塔在东北方向,B见塔在正东方向,C见塔在南偏东60°方向.求塔到直路的距离.
[分析与解答]
|