![]()

 (教师独具内容)
(教师独具内容)
课程标准:1.通过实例,了解集合的含义,理解元素与集合的属于关系.2.针对具体问题,能在自然语言和图形语言的基础上,用符号语言刻画集合.
教学重点:1.集合概念的正确理解.2.元素的三性(确定性、互异性、无序性).3.元素与集合关系的判定.4.集合常用的两种表示方法(列举法、描述法).
教学难点:1.对元素的确定性的理解.2.描述法表示集合.

【知识导学】
知识点 一 集合与元素的定义
一 集合与元素的定义
元素:一般地,我们把研究对象统称为元素(element).
集合:把一些元素组成的01总体叫做集合(set)(简称为集).
表示:通常用大写拉丁字母A,B,C,…表示集合,用小写拉丁字母a,b,c,…表示集合中的元素.
知识点 二 集合中元素的三个特性
二 集合中元素的三个特性
(1)确定性;
(2)互异性;
(3)无序性.
知识点 三 元素与集合的关系
三 元素与集合的关系
(1)“属于”:如果a是集合A的元素,就说a属于集合A,记作01a∈A.
(2)“不属于”:如果a不是集合A中的元素,就说a不属于集合A,记作02a∉A.
知识点 四 几个常用数集的固定字母表示
四 几个常用数集的固定字母表示
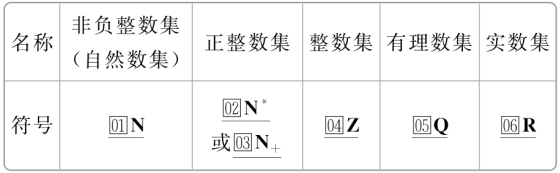
知识点 五 集合的表示方法
五 集合的表示方法
集合常见的表示方法有:01自然语言、02列举法、03描述法.
(1)自然语言:用文字叙述的形式描述集合的方法.使用此方法时,只要叙述清楚即可,如由所有正方形构成的集合,就是用自然语言表示的,不能叙述成“正方形”.再如全体实数组成的集合,或实数集等.
(2)列举法:把集合的所有元素04一一列举出来,并用花括号“{ }”括起来表示集合的方法叫做列举法.
(3)描述法:一般地,设A是一个集合,我们把集合A中所有具有共同特征P(x)的元素x所组成的集合表示为05{x∈A|P(x)},这种表示集合的方法称为描述法.
知识点 六 集合的分类
六 集合的分类
(1)有限集;
(2)无限集.
【新知拓展】
1.元素和集合关系的判断
(1)直接法:如果集合中的元素是直接给出的,只要判断该元素在已知集合中是否出现即可.此时应先明确集合是由哪些元素构成的.
(2)推理法:对于某些不便直接表示的集合,只要判断该元素是否满足集合中元素所具有的特征即可.此时应先明确已知集合的元素具有什么特征,即该集合中元素要满足哪些条件.
2.集合的三个特性
(1)描述性:“集合”是一个原始的不加定义的概念,它同平面几何中的“点”“线”“面”等概念一样都只是描述性的说明.
(2)整体性:集合是一个整体,暗含“所有”“全部”“全体”的含义,因此一些对象一旦组成了集合,这个集合就是这些对象的总体.
(3)广泛性:组成集合的对象可以是数、点、图形、多项式、方程,也可以是人或物,甚至一个集合也可以是某集合的一个元素.
3.使用列举法表示集合时需注意的几点
(1)元素之间用“,”隔开;
(2)元素不重复,满足元素的互异性;
(3)元素无顺序,满足元素的无序性;
(4)对于含较多元素的集合,如果构成该集合的元素有明显规律,可用列举法,但是必须把元素间的规律表述清楚后才能用省略号.

1.判一判(正确的打“√”,错误的打“×”)
(1)某校高一年级16岁以下的学生能构成集合.( )
(2)已知A是一个确定的集合,a是任一元素,要么a∈A,要么a∉A,二者必居其一且只具其一.( )
(3)对于数集A={1,2,x2},若x∈A,则x=0.( )
(4)集合{y|y=x2,x∈R}与集合{s|s=t2,t∈R}的元素完全相同.( )
答案 (1)√ (2)√ (3)× (4)√
2.做一做
(1)下列所给的对象能组成集合的是( )
A.“金砖国家”成员国 B.接近1的数
C.著名的科学家 D.漂亮的鲜花
(2)用适当的符号(∈,∉)填空:
0________∅,0________{0},0________N,
-2________N*,3________Z,________Q,
π________R.
答案 (1)A (2)∉ ∈ ∈ ∉ ∉ ∉ ∈

题型一 正确理解描述法中元素的“代表符号”
例1 分析下列集合中的元素是什么?
A={x|y=x2},B={y|y=x2},C={(x,y)|y=x2}.
[解] 三个集合都是用描述法表示的.对于集合A,其中的元素是x,根据“y=x2”,这里的x并没有什么限制,即x可以是任意实数,即集合A是由所有实数组成的集合,即实数集.对于集合B,其中的元素是y,这里的x没有任何限制,即x可以是任意实数,但是通过“y=x2”,元素y有了限制:实数的平方,从而B中的元素是非负实数.对于集合C,从元素的代表符号“(x,y)”可以看出,其中的元素是有序实数对,这些数对的第一个数x没有限制,第二个数y受条件“y=x2”的限制,因此C中的元素是有序实数对,且数对的第一个数取任意实数,第二个数是第一个数的平方(从几何角度讲,(x,y)就是坐标平面内的一个点,从而C中的元素就是抛物线y=x2上的点).
金版点睛
使用描述法表示集合时要注意:①写清该集合中元素的代表符号,如{x∈R|x>1}不能写成{x>1};②用简明、准确的语言进行描述,如方程、不等式、几何图形等;③不能出现未被说明的字母,如{x∈Z|x=2m}中m未被说明,故此集合中的元素是不确定的;④所有描述的内容都要写在花括号内,如“{x∈Z|x=2m},m∈N*”不符合要求,应将“m∈N*”写进“{ }”中,即{x∈Z|x=2m,m∈N*};⑤元素的取值(或变化)范围,从上下文的关系来看,若x∈R是明确的,则x∈R可省略不写,如集合D={x∈R|x<10}也可表示为D={x|x<10};⑥多层描述时,应当准确使用“且”“或”等表示元素之间关系的词语,如“{x|x<-1或x>1}”等.
试分析集合{(x,y)|y=x+1}的元素,并能从几何角度解释这个集合.
解 集合中的元素是有序实数对,且第二个实数等于第一个实数加1.
从几何角度:该集合就是一次函数y=x+1的图象,即直线y=x+1.
题型二 判断元素与集合的关系
例2 已知集合A={x|x=m+n·,m,n∈Z}.
(1)判断0,(1+)2,2与A的关系;
(2)若x1,x2∈A,试探究x1x2,x1+x2与A的关系.
[解] (1)易知0=0+0×,且0∈Z,
所以0∈A.
因为(1+)2=3+2,且3,2∈Z,
所以(1+)2∈A.
因为2=()()2=7+7,
且7,7∉Z,所以2∉A.
(2)因为x1,x2∈A,所以可设x1=m1+n1,x2=m2+n2,且m1,n1,m2,n2∈Z,
所以x1x2=(m1+n1)(m2+n2)=m1m2+(m2n1+m1n2)+2n1n2=(m1m2+2n1n2)+(m2n1+m1n2).因为m1m2+2n1n2∈Z,m2n1+m1n2∈Z,所以x1x2∈A.
因为x1+x2=(m1+m2)+(n1+n2),m1+m2∈Z,n1+n2∈Z,所以x1+x2∈A.
金版点睛
该问题是判断所给的元素是否具有集合A中元素的特征,用自然语言理解为:所给元素是否能写成“整数+整数的倍”的形式.可以看出,问题的实质是正确解读集合的表示方法(描述法).
已知集合A=∈Z,试判断-2,2与A的关系.
解 解法一:易知A={-3,0,1,2,4,5,6,9},
所以-2∉A,2∈A.
解法二:当x=-2时,3-x=5∉Z,所以-2∉A;
当x=2时,x∈Z且3-x=6∈Z,所以2∈A.
题型三 含参问题探究
例3 集合A={x|kx2-8x+16=0},若集合A只有一个元素,试求实数k的值,并用列举法表示集合A.
[解] ①当k=0时,原方程为16-8x=0,
∴x=2,此时A={2}.
②当k≠0时,若集合A中只有一个元素,
则方程kx2-8x+16=0有两个相等实根.
即Δ=64-64k=0,即k=1,
从而x1=x2=4,
∴集合A={4}.
综上所述,实数k的值为0或1.当k=0时,A={2};
当k=1时,A={4}.
金版点睛
对于含参问题,随着参数值的变化,问题的解发生变化,所以这类问题往往需要分类讨论.通过分类,把复杂的问题简单化,从而蕴含着转化的数学思想.
把本例条件“只有一个元素”改为“有两个元素”,求实数k的取值范围的集合.
解 由题意可知方程kx2-8x+16=0有两个不等的实根.
∴Δ=64-64k>0,解得k<1且k≠0.
∴实数k的取值范围的集合为{k|k<1且k≠0}.
题型四 集合中的新定义问题
例4 已知集合A={1,2,4},则集合B={(x,y)|x∈A,y∈A}中元素的个数为( )
A.3 B.6
C.8 D.9
[解析] 根据已知条件,列表如下:
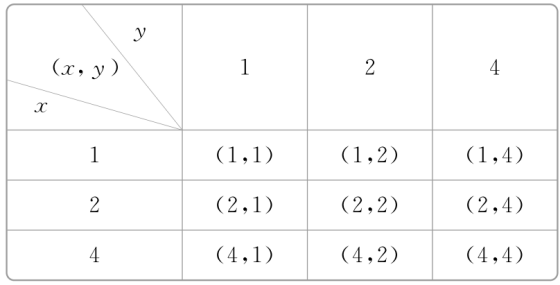
由上表可知,B中的元素有9个,故选D.
[答案] D
金版点睛
本例借助表格语言,运用列举法求解.表格语言是常用的数学语言,表达问题清晰,明了;列举法是分析问题的重要的数学方法,通过“列举”直接解决问题或发现问题的规律,此方法通常配合图表(含树形图)使用.
定义A*B={z|z=xy,x∈A,y∈B},设A={1,2},B={0,2},则集合A*B中的所有元素之和为( )
A.0 B.2
C.3 D.6
答案 D
解析 根据已知条件,列表如下:
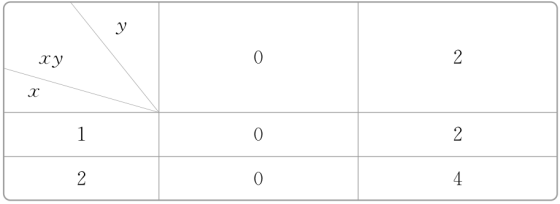
根据集合中元素的互异性,可由上表知A*B={0,2,4},故其中所有元素之和为0+2+4=6,故选D.

1.下列所给的对象不能组成集合的是( )
A.我国古代的四大发明
B.二元一次方程x+y=1的解
C.某班年龄较小的同学
D.平面内到定点距离等于定长的点
答案 C
解析 C项中“年龄较小的同学”的标准不明确,不符合确定性,故选C.
2.已知集合A含有三个元素2,4,6,且当a∈A时,有6-a∈A,则a为( )
A.2 B.2或4
C.4 D.0
答案 B
解析 集合A中含有三个元素2,4,6,且当a∈A,有6-a∈A.当a=2∈A时,6-a=4∈A,∴a=2;当a=4∈A时,6-a=2∈A,∴a=4;当a=6∈A时,6-a=0∉A,综上所述,a=2或4.故选B.
3.由实数-a,a,|a|,所组成的集合最多含有的元素个数是( )
A.1 B.2
C.3 D.4
答案 B
解析 对a进行分类讨论:①当a=0时,四个数都为0,只含有一个元素;②当a≠0时,含有两个元素a,-a,所以集合中最多含有2个元素.故选B.
4.用适当符号(∈,∉)填空:
(1)(1,3)________{(x,y)|y=2x+1};
(2)2________{m|m=2(n-1),n∈Z}.
答案 (1)∈ (2)∈
解析 (1)当x=1时,y=2×1+1=3,故(1,3)∈{(x,y)|y=2x+1}.
(2)当n=2∈Z时,m=2×(2-1)=2,故2∈{m|m=2(n-1),n∈Z}.
5.设a∈R,关于x的方程(x-1)(x-a)=0的解集为A,试分别用描述法和列举法表示集合A.
解 A={x|(x-1)(x-a)=0};当a=1时,A={1};当a≠1时,A={1,a}.