![]()

![]() 3.1.1 函数的概念
3.1.1 函数的概念
![]() (教师独具内容)
(教师独具内容)
课程标准:1.通过丰富实例,进一步体会函数是描述变量之间的依赖关系的重要数学模型.2.在此基础上学习用集合与对应的符号语言来刻画函数,体会对应关系在刻画函数概念中的作用.3.了解构成函数的要素,能求一些简单函数的定义域.
教学重点:1.理解函数的定义,会求一些简单函数的定义域和值域.2.明确函数的两个要素,了解同一个函数的定义,会判定两个给定的函数是否是同一个函数.
教学难点:1.对应关系f的正确理解,函数符号y=f(x)的理解.2.抽象函数的定义域.3.一些简单函数值域的求法.
![]()
【知识导学】
知识点一 函数的概念
一般地,设A,B是非空的实数集,如果对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有01唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作02y=f(x),x∈A.其中,x叫做03自变量,x的取值范围A叫做函数的04定义域;与x的值相对应的y值叫做05函数值,函数值的集合{f(x)|x∈A}叫做函数的06值域.显然,07值域是集合B的子集.
注意:(1)两个非空实数集间的对应能否构成函数,主要看是否满足三性:任意性、存在性、唯一性.这是因为函数概念中明确要求对于非空实数集A中的任意一个(任意性)元素x,在非空实数集B中都有(存在性)唯一(唯一性)的元素y与之对应.这三性只要有一个不满足便不能构成函数.
(2)集合A是函数的定义域,因为给定A中每一个x值都有唯一的y值与之对应;集合B不一定是函数的值域,因为B中的元素可以在A中没有与之对应的x,也就是说,B中的某些元素可以不是函数值,即{f(x)|x∈A}⊆B.
(3)在函数定义中,我们用符号y=f(x)表示函数,其中f(x)表示“x对应的函数值”,而不是“f乘x”.
知识点二 函数的两要素
从函数的定义可以看出,函数有三个要素:01定义域、02对应关系、03值域,由于值域是由定义域和对应关系决定的,所以确定一个函数只需要两个要素:04定义域和对应关系.即要检验给定的两个变量(变量均为数值)之间是否具有函数关系,只要检验:
(1)定义域和对应关系是否给出;
(2)根据给出的对应关系,自变量x在其定义域中的每一个值是否都有唯一的函数值y和它对应.
知识点三 区间的概念
(1)设a,b是两个实数,而且a<b.我们规定:
①满足不等式a≤x≤b的实数x的集合叫做01闭区间,表示为02[a,b];
②满足不等式a<x<b的实数x的集合叫做03开区间,表示为04(a,b);
③满足不等式a≤x<b或a<x≤b的实数x的集合叫做05半开半闭区间,分别表示为06[a,b),(a,b].
这里的实数a与b都叫做相应区间的07端点.
实数集R可以用区间表示为08(-∞,+∞),“∞”读作“09无穷大”,“-∞”读作“10负无穷大”,“+∞”读作“11正无穷大”.
我们可以把满足x≥a,x>a,x≤b,x<b的实数x的集合,用区间分别表示为12[a,+∞),13(a,+∞),14(-∞,b],15(-∞,b).
(2)区间的几何表示
在用数轴表示区间时,用实心点表示16包括在区间内的端点,用空心点表示17不包括在区间内的端点.
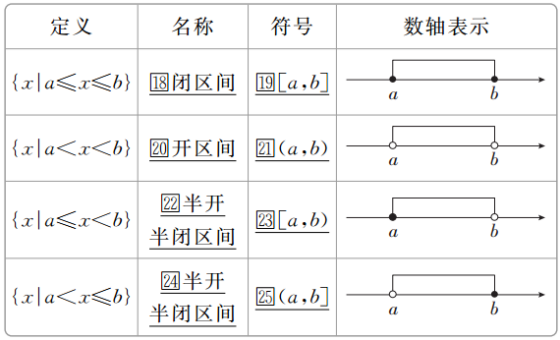
(3)含“∞”的区间的几何表示
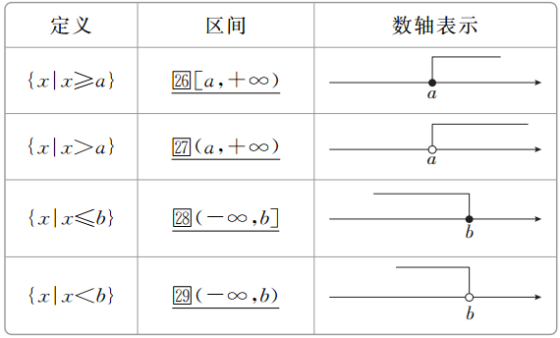
注意:(1)无穷大“∞”只是一个符号,而不是一个数,因而它不具备数的一些性质和运算法则.
(2)以“-∞”或“+∞”为区间一端时,这一端必须用小括号.
知识点四 同一个函数
如果两个函数的01定义域相同,并且02对应关系完全一致,即相同的03自变量对应的04函数值也相同,那么这两个函数是同一个函数.
【新知拓展】
(1)函数符号“y=f(x)”是数学中抽象符号之一,“y=f(x)”仅为y是x的函数的数学表示,不表示y等于f与x的乘积,f(x)也不一定是解析式,还可以是图表或图象.
(2)函数的概念中强调“三性”:任意性、存在性、唯一性,这是因为函数定义中明确要求是对于非空实数集A中的任意一个(任意性)数x,在非空实数集B中都有(存在性)唯一确定(唯一性)的数y和它对应,这“三性”只要有一个不满足,便不能构成函数.
![]()
1.判一判(正确的打“√”,错误的打“×”)
(1)函数值域中的每一个数都有定义域中的数与之对应.( )
(2)函数的定义域和值域一定是无限集合.( )
(3)定义域和对应关系确定后,函数值域也就确定了.( )
(4)若函数的定义域中只有一个元素,则值域中也只有一个元素.( )
(5)对于定义在集合A到集合B上的函数y=f(x),x1,x2∈A,若x1≠x2,则f(x1)≠f(x2).( )
答案 (1)√ (2)× (3)√ (4)√ (5)×
2.做一做(请把正确的答案写在横线上)
(1)下列给出的对应关系f,不能确定从集合A到集合B的函数关系的是________.
①A={1,4},B={-1,1,-2,2},对应关系:开平方;
②A={0,1,2},B={1,2},对应关系:
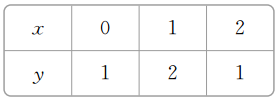
③A=[0,2],B=[0,1],对应关系:
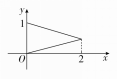
(2)下列函数中,与函数y=x是同一个函数的是________.
①y=;②y=x3;③y=()2;④s=t.
答案 (1)①③ (2)②④
![]()
题型一 求函数的定义域
例1 求下列函数的定义域:
(1)y=2x+3;(2)f(x)=x+1;(3)y=+;(4)y=x2-1;(5)y=(1-2x)0.
[解] (1)函数y=2x+3的定义域为{x|x∈R}.
(2)要使函数式有意义,即分式有意义,则x+1≠0,x≠-1.故函数的定义域为{x|x≠-1}.
(3)要使函数式有意义,则1-x≥0,即x≤1,所以x=1,从而函数的定义域为{x|x=1}.
(4)因为当x2-1≠0,即x≠±1时,x2-1有意义,所以函数的定义域是{x|x≠±1}.
(5)∵1-2x≠0,即x≠2,
∴函数的定义域为x≠2}.
例2 已知函数f(x)的定义域是[-1,4],求函数f(2x+1)的定义域.
[解] 已知函数f(x)的定义域是[-1,4],即-1≤x≤4.
故对于f(2x+1)应有-1≤2x+1≤4.
∴-2≤2x≤3,∴-1≤x≤2,
∴函数f(2x+1)的定义域是2.
例3 如图所示,用长为1 m的铁丝做一个下部为矩形、上部为半圆形的框架(铁丝恰好用完),若半圆的半径为x(单位:m),求此框架围成的面积y(单位:m2)与x的函数关系式.
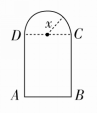
[解] 由题意可得,AB=2x,︵的长为πx,
于是AD=2,
∴y=2x·2+2,即y=-2x2+x.
由>0,得0<x<π+2,
∴此函数的定义域为π+2.
故所求的函数关系式为y=-2x2+xπ+2.
金版点睛
求函数定义域的基本要求
(1)整式:若y=f(x)为整式,则函数的定义域是实数集R.
(2)分式:若y=f(x)为分式,则函数的定义域为使分母不为0的实数集.
(3)偶次根式:若y=f(x)为偶次根式,则函数的定义域为被开方数非负的实数集(特别注意0的0次幂没有意义).
(4)几部分组成:若y=f(x)是由几部分数学式子的和、差、积、商组成的形式,定义域是使各部分都有意义的集合的交集.
(5)对于抽象函数的定义域:
①若f(x)的定义域为[a,b],则f[g(x)]中,g(x)∈[a,b],从中解得x的解集即f[g(x)]的定义域.
②若f[g(x)]的定义域为[m,n],则由x∈[m,n]可确定g(x)的范围,设u=g(x),则f[g(x)]=f(u),又f(u)与f(x)是同一个函数,所以g(x)的范围即f(x)的定义域.
③已知f[φ(x)]的定义域,求f[h(x)]的定义域,先由f[φ(x)]中x的取值范围,求出φ(x)的取值范围,即f(x)中的x的取值范围,即h(x)的取值范围,再根据h(x)的取值范围便可以求出f[h(x)]中x的取值范围.
(6)实际问题:若y=f(x)是由实际问题确定的,其定义域要受实际问题的约束.如:例3中,任何一条线段的长均大于零.
(1)若函数f(x+1)的定义域为,2,则函数f(x-1)的定义域为________;
(2)求下列函数的定义域:
①y=()x+1-;②y=|x|-x;
(3)①求函数y=+-x2-9的定义域;
②将长为a m的铁丝折成矩形(铁丝恰好用完),求矩形的面积y(单位:m2)关于一边长x(单位:m)的解析式,并写出此函数的定义域.
答案 (1),4 (2)见解析 (3)见解析
解析 (1)由题意知,-2≤x≤2,则2≤x+1≤3,
即f(x)的定义域为,3,∴2≤x-1≤3,
解得2≤x≤4.∴f(x-1)的定义域为,4.
(2)①要使函数有意义,自变量x的取值必须满足1-x≥0,即x≤1,
∴函数的定义域为{x|x≤1,且x≠-1}.
②要使函数有意义,需满足|x|-x≠0,即|x|≠x,
∴x<0.
∴函数的定义域为{x|x<0}.
(3)①解不等式组x2-9≠0,得x≠±3.
故函数的定义域是{x|1≤x≤5,且x≠3}.
②因为矩形的一边长为x,则另一边长为2(a-2x),
所以y=x·2(a-2x)=-x2+2ax,
定义域为2.
题型二 已知函数值求自变量的值
例4 已知函数f(x)=2x2-4,x∈R,若f(x0)=2,求x0的值.
[解] 易知f(x0)=2x0-4,
∴2x0-4=2,即x0=3.
又∵x0∈R,∴x0=±.
金版点睛
就本例而言,已知函数值求自变量的值就是解方程,需要注意:所求的自变量的值必须在函数的定义域内.如果本例中加一个条件“x∈[0,+∞)”,则x0=(-不符合题意,舍去).
已知函数f(x)=x2-2x,x∈(-∞,0),若f(x0)=3.求x0的值.
解 由题意可得f(x0)=x0-2x0.
∴x0-2x0=3,即x0-2x0-3=0.
解得x0=3或x0=-1.
又∵x0∈(-∞,0),∴x0=-1.
题型三 已知自变量的值求函数值
例5 已知f(x)=x2,x∈R,求:
(1)f(0),f(1);
(2)f(a),f(a+1).
[解] (1)f(0)=02=0,f(1)=12=1.
(2)∵a∈R,a+1∈R,
∴f(a)=a2,f(a+1)=(a+1)2.
金版点睛
对于函数定义域内的每一个值,都可以求函数值(当然函数值唯一),本例可以直接应用公式:f(x)=x2求解,实质上就是求代数式的值,例如f(1)就是当x=1时,代数式x2的值,而f(a+1)就是当x=a+1时,代数式x2的值.
已知f(x)=+x+1,求:
(1)f(2);
(2)当a>0时,f(a+1)的值.
解 (1)f(2)=+3.
(2)易知f(x)的定义域A=[0,+∞),
∵a>0,∴a+1>1,则a+1∈A,
∴f(a+1)=+a+2.
题型四 求函数的值域
例6 求下列函数的值域:
(1)y=x+1,x∈{1,2,3,4,5};
(2)y=x2-2x+3,x∈[0,3);
(3)y=x-3;
(4)y=2x-.
[解] (1)(观察法)因为x∈{1,2,3,4,5},分别代入求值,可得函数的值域为{2,3,4,5,6}.
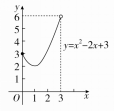
(2)(配方法)y=x2-2x+3=(x-1)2+2,由x∈[0,3),再结合函数的图象(如图),可得函数的值域为[2,6).
(3)(分离常数法)y=x-3=()x-3=2+x-3,
显然x-3≠0,所以y≠2.
故函数的值域为(-∞,2)∪(2,+∞).
(4)(换元法)设t=,则x=t2+1,且t≥0,
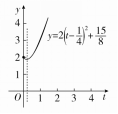
所以y=2(t2+1)-t
=242+8,
由t≥0,再结合函数的图象(如右图),可得函数的值域为,+∞.
金版点睛
求函数值域的原则及常用方法
(1)原则:①先确定相应的定义域;②再根据函数的具体形式及运算法则确定其值域.
(2)常用方法
①观察法:对于一些比较简单的函数,其值域可通过观察法得到.
②配方法:是求“二次函数”类值域的基本方法.
③换元法:运用新元代换,将所给函数化成值域易确定的函数,从而求得原函数的值域.对于f(x)=ax+b+(其中a,b,c,d为常数,且ac≠0)型的函数常用换元法.
④分离常数法:此方法主要是针对有理分式,即将有理分式转化为“反比例函数类”的形式,便于求值域.
求下列函数的值域:
(1)y=x+1;
(2)y=x2-4x+6,x∈[1,5);
(3)y=x+.
解 (1)∵y=x+1=()x+1=1-x+1,且x+1≠0,
∴函数y=x+1的值域为{y|y≠1}.
(2)配方,得y=(x-2)2+2.
∵x∈[1,5),
∴结合函数的图象可知,函数的值域为{y|2≤y<11}.
(3)(换元法)设t=,则x=t2-1,且t≥0,
所以y=t2+t-1=22-4,
由t≥0,再结合函数的图象可得函数的值域为[-1,+∞).
题型五 相同函数的判断
例7 下列各组函数表示同一函数的是( )
A.f(x)=x,g(x)=()2
B.f(x)=x2+1,g(t)=t2+1
C.f(x)=1,g(x)=x
D.f(x)=x,g(x)=|x|
[解析] A项中,由于f(x)=x的定义域为R,g(x)=()2的定义域为{x|x≥0},它们的定义域不相同,所以它们不是同一函数.
B项中,函数的定义域、值域和对应关系都相同,所以它们是同一函数.
C项中,由于f(x)=1的定义域为R,g(x)=x的定义域为{x|x≠0},它们的定义域不相同,所以它们不是同一函数.
D项中,两个函数的定义域相同,但对应关系不同,所以它们不是同一函数.
[答案] B
金版点睛
判断两个函数为同一函数的条件
(1)判断两个函数是相同函数的准则是两个函数的定义域和对应关系分别相同.定义域、对应关系两者中只要有一个不相同就不是相同函数,即使定义域与值域都相同,也不一定是相同函数.
(2)函数是两个实数集之间的对应关系,所以用什么字母表示自变量、因变量是没有限制的.另外,在化简解析式时,必须是等价变形.
下列函数中哪个与函数y=x相同?
(1)y=()2;(2)y=x3;(3)y=;(4)y=x.
解 (1)y=()2=x(x≥0),y≥0,定义域不同且值域不同,所以不相同.
(2)y=x3=x(x∈R),y∈R,对应关系相同,定义域和值域都相同,所以相同.
(3)y==|x|=-x,x<0,y≥0;值域不同,且当x<0时,它的对应关系与函数y=x不相同,所以不相同.
(4)y=x的定义域为{x|x≠0},与函数y=x的定义域不相同,所以不相同.
![]()
1.下列各图中,可能是函数y=f(x)的图象的是( )
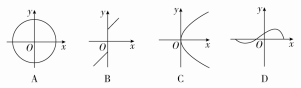
答案 D
解析 A,B中的图象与y轴有两个交点,即有两个y值与x=0对应,所以A,B不可能是函数y=f(x)的图象;对于C中图象,过x=1作与x轴垂直的直线,与图象有两个交点,所以C不可能是函数y=f(x)的图象.故选D.
2.函数f(x)=x+的定义域是( )
A.{x|x≥2} B.{x|x>2}
C.{x|x≤2} D.{x|x<2}
答案 C
解析 要使函数式有意义,则2-x≥0,即x≤2.所以函数的定义域为{x|x≤2}.
3.已知函数f(x)的定义域为(-1,0),则函数f(2x+1)的定义域为( )
A.(-1,1) B.2
C.(-1,0) D.,1
答案 B
解析 ∵原函数的定义域为(-1,0),
∴-1<2x+1<0,解得-1<x<-2.
∴函数f(2x+1)的定义域为2.
4.已知函数f(x)=x2-2ax+5的定义域和值域都是[1,a],则a=________.
答案 2
解析 因为f(x)=(x-a)2+5-a2,所以f(x)在[1,a]上是减函数,又f(x)的定义域和值域均为[1,a],所以()()fa=1,即a2-2a2+5=1,解得a=2.
5.已知函数f(x)=x2+x-1.
(1)求f(2),fx,f(a+1);
(2)若f(x)=5,求x.
解 (1)f(2)=22+2-1=5,
fx=x2+x-1=x2,
f(a+1)=(a+1)2+(a+1)-1=a2+3a+1.
(2)∵f(x)=x2+x-1=5,∴x2+x-6=0,解得x=2或x=-3.