4.1.1　n次方根与分数指数幂

(教师独具内容)

课程标准：1.理解根式的定义和性质、分数指数幂的定义.2.把握分式与负整数指数幂、根式与正分数指数幂的内在联系．

教学重点：1.根式的定义和性质.2.根式与分数指数幂的联系.3.正分数指数幂与负分数指数幂的联系．

教学难点：1.指数幂的含义及其与根式的互化.2.an(n)与(a(n))ⁿ的区别与联系．

【知识导学】

知识点一　根式的定义

(1)a的n次方根的定义：01(□)一般地，如果xⁿ＝a，那么x叫做a的n次方根，其中n＞1，且n∈N^*.

(2)a的n次方根的表示

①当n是奇数时，02(□)a的n次方根表示为a(n)，a∈R；

②当n是偶数时，03(□)a的n次方根表示为±a(n)，其中－a(n)表示a的负的n次方根，a∈[0，＋∞)．

(3)根式：04(□)式子a(n)叫做根式，这里n叫做根指数，a叫做被开方数．

知识点二　根式的性质

(1)(a(n))ⁿ＝01(□)a(n为奇数时，a∈R；n为偶数时，a≥0，且n＞1)．

(2)an(n)＝02(□)()()|a|n为偶数，且n＞1(an为奇数，且n＞1，).

知识点三　分数指数幂的意义

(1)an(m)n(m)＝01(□) am(n)，an(m)n(m)＝n(m)n(m) (m)＝02(□)am(n)(其中a>0，m，n∈N^*，且n>1)．

(2)0的正分数指数幂等于03(□)0,0的负分数指数幂04(□)没有意义．

知识点四　有理数指数幂的运算性质

(1)a^ra^s＝01(□)a^r＋s(a>0，r，s∈Q)．

(2)(a^r)^s＝02(□)a^rs(a>0，r，s∈Q)．

(3)(ab)^r＝03(□)a^rb^r(a>0，b>0，r∈Q)．

【新知拓展】

1.an(n)与(a(n))ⁿ的区别

(1)an(n)是实数aⁿ的n次方根，是一个恒有意义的式子，不受n的奇偶限制，但这个式子的值受n的奇偶限制．其算法是对a先乘方，再开方(都是n次)，结果不一定等于a，当n为奇数时，an(n)＝a；当n为偶数时，an(n)＝|a|＝－a，a<0.(a，a≥0，)

(2)(a(n))ⁿ是实数a的n次方根的n次幂，其中实数a的取值范围由n的奇偶决定．其算法是对a先开方，后乘方(都是n次)，结果恒等于a.

2.分数指数幂的理解

(1)分数指数幂是指数概念的又一推广，分数指数幂an(m)n(m)不可理解为n(m)个a相乘，它是根式的一种新的写法．在这样的规定下，根式与分数指数幂是表示相同意义的量，只是形式不同而已．

(2)把根式 am(n)化成分数指数幂的形式时，不要轻易对n(m)进行约分．

3.在保证相应的根式有意义的前提下，负数也存在分数指数幂，如(－5) 3(2)3(2)＝()－52(3)有意义，但(－5) 4(3)4(3)＝()－53(4)就没有意义．

1.判一判(正确的打“√”，错误的打“×”)

(1)因为3²＝9，所以3是9的平方根．(　　)

(2)当n∈N^*时，(－16(n))ⁿ都有意义．(　　)

(3) ()＝π－3.(　　)

答案　(1)√　(2)×　(3)√

2.做一做(请把正确的答案写在横线上)

(1)用根式的形式表示下列各式(a>0)：

①a5(1)5(1)＝________；②a4(3)4(3)＝________；

③a5(3)5(3)＝________；④a3(2)3(2)＝________.

(2)将下列根式写成分数指数幂的形式(其中a>b>0)．

① ()a－b7(5)＝________；② ()a2－b23(4)＝________；

③ a2b－ab2(4)＝________；④ ()a2－b22(4)＝________.

(3)若n为偶数时， ()x－1n(n)＝x－1，则x的取值范围为________．

答案　(1)①a(5)　②a3(4)　③a3(5)　④a2(3)

 (2)①(a－b) 5(7)5(7)　②(a²－b²) 4(3)4(3)　③(a²b－ab²) 4(1)4(1)　④(a²－b²) 4(2)4(2)　(3)x≥1

题型一   根式的概念　利用根式的性质化简

例1　(1)①16的平方根为________，－27的5次方根为________；

②已知x⁷＝6，则x＝________；

③若x－2(4)有意义，则实数x的取值范围是________；

(2)化简：① ()x－πn(n)(x<π，n∈N^*)；

② 2(1).

[解析]　(1)①∵(±4)²＝16，∴16的平方根为±4.－27的5次方根为－27(5).

②∵x⁷＝6，∴x＝6(7).

③要使x－2(4)有意义，则需x－2≥0，即x≥2.因此实数x的取值范围是[2，＋∞)．

(2)①∵x<π，∴x－π<0，

当n为偶数时， ()x－πn(n)＝|x－π|＝π－x；

当n为奇数时， ()x－πn(n)＝x－π.

综上， ()x－πn(n)＝x－π，n为奇数，n∈N*.(π－x，n为偶数，n∈N*，)

②∵a≤2(1)，∴1－2a≥0，

∴ ＝()＝|2a－1|＝1－2a.

[答案]　(1)①±4　－27(5)　②6(7)　③[2，＋∞)

(2)见解析

金版点睛

1.判断关于n次方根的结论应关注的两点

(1)n的奇偶性决定了n次方根的个数；

(2)n为奇数时，a的正负决定着n次方根的符号．

2.根式化简求值解题思路

解决根式的化简问题，首先要分清根式为奇次根式还是偶次根式，然后运用根式的性质进行解答.

　(1)下列说法正确的个数是(　　)

①16的4次方根是2；②16(4)的运算结果是±2；③当n为大于1的奇数时，a(n)对任意a∈R都有意义；④当n为大于1的偶数时，a(n)只有当a≥0时才有意义．

A.1  B．2  C．3  D．4

(2)已知m¹⁰＝2，则m等于(　　)

A.2(10)  B．－2(10)  C.  D．±2(10)

(3)化简下列各式：

①－27(3)；②(－9(3))³；③ ().

答案　(1)B　(2)D　(3)见解析

解析　(1)①16的4次方根应是±2；②16(4)＝2，③④正确．

(2)∵m¹⁰＝2，∴m是2的10次方根．又∵10是偶数，∴2 的10次方根有两个，且互为相反数，

∴m＝±2(10).

(3)①－27(3)＝()－33(3)＝－3.

②(－9(3))³＝－9.

③ ()＝|a－b|＝()()b－aa<b.(a－ba≥b，)

题型二  根式与分数指数幂的互化

例2　下列根式与分数指数幂的互化中，正确的是(　　)

A.－x(4)＝(－x) 4(1)4(1) (x>0)

B.x5(1)5(1)＝－x(5)(x≠0)

C.y(x) 4(3)4(3)＝3(y)(xy>0)

D.y2(8)＝y4(1)4(1)

[解析]　对于A，－x(4)＝－x4(1)4(1)，所以A错误；对于B，x5(1)5(1)＝x(5)，所以B错误；对于C，y(x)4(3)4(3)＝ 3(y)(xy>0)，所以C正确；对于D，y2(8)＝|y|4(1)4(1)，所以D错误．

[答案]　C

金版点睛

根式与分数指数幂互化依据

(1)在解决根式与分数指数幂互化的问题时，关键是熟记根式与分数指数幂的转化式子：an(m)n(m)＝am(n)和an(m)n(m)＝n(m)n(m) (m)＝ am(n)，其中字母a要使式子有意义．

(2)将含有多重根号的根式化为分数指数幂的途径有两条：一是由里向外化为分数指数幂；二是由外向里化为分数指数幂.

　用分数指数幂表示下列各式：

(1) ()3(3)(a>0，b>0)；

(2)()2(5)(x>0)．

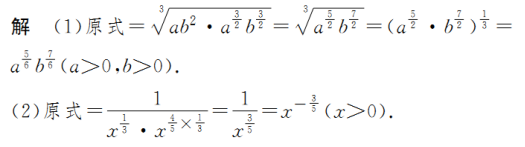
题型三  多重根式的化简

例3　化简： ＋ .

[解]　解法一：

原式＝ ()＋ ()

＝ ()＋ ()

＝ ＋1＋－1＝2.

解法二：令x＝＋，两边平方得x²＝6＋2＝8.因为x>0，所以x＝2.

金版点睛

形如 (m>0，n>0)的双重根式，一般是将其转化为()的形式后再化简．由于(±)²＝a＋b±2，因此转化的方法就是寻找a，b，使得ab＝n，(a＋b＝m，)即a，b是方程x²－mx＋n＝0的两个根．如化简，首先化为的形式，即2(3)，解方程x²－4x＋3＝0，得x＝3或x＝1，则4－2＝(－1)²，所以＝2(3)＝()2(3－12)＝2(3－1)＝2(2).

　化简： － ＋ .

解　原式＝ ()－ ()＋ ()

＝＋－(2－)＋2－＝2.

1.已知x⁵＝6，则x等于(　　)

A.  B.6(5)  C．－6(5)  D．±6(5)

答案　B

解析　由根式的定义知，x⁵＝6，x＝6(5)，选B.

2.下列各式正确的是(　　)

A.()＝－3   B.a4(4)＝a

C.＝2   D.()－23(3)＝2

答案　C

解析　由于()＝3，a4(4)＝|a|，()－23(3)＝－2，故A，B，D错误.

3.若 4a2－4a＋1(6)＝1－2a(3)，则实数a的取值范围是(　　)

A.(－∞，2)   B.，＋∞(1)

C.，＋∞(1)   D.2(1)

答案　D

解析　∵4a2－4a＋1(6)＝ ()2a－12(6)＝ ()1－2a2(6)＝1－2a(3)，∴1－2a≥0，即a≤2(1).

4.计算下列各式的值：

(1) －53(3)＝__________；

(2)设b<0，则()²＝__________.

答案　(1)－5　(2)－b

解析　(1) －53(3)＝－53(3)＝－5.

(2)∵b<0，∴－b>0，∴()²＝－b.

5.计算： ()＋()(e≈2.7)．

解　原式＝＋＝

()＋()＝e－e^－1＋e＋e^－1＝2e≈5.4.