4.4.3　不同函数增长的差异

(教师独具内容)

课程标准：利用计算器、计算机画出幂函数、指数函数、对数函数的图象，探索、比较它们的变化规律．

教学重点：比较一次函数、指数函数、对数函数增长的快慢差异，结合实例体会直线上升、指数爆炸、对数增长等不同函数类型增长的含义．

教学难点：指数函数、幂函数不同区间增长快慢的差异.

【知识导学】

知识点　几种函数模型的增长差异

(1)当a＞1时，指数函数y＝a^x是01(□)增函数，并且当a越02(□)大时，其函数值的增长就越快．

(2)当a＞1时，对数函数y＝log_ax是03(□)增函数，并且当a越04(□)小时，其函数值的增长就越快．

(3)当x＞0，n＞1时，幂函数y＝xⁿ显然也是05(□)增函数，并且当x＞1时，n越06(□)大，其函数值的增长就越快．

(4)一般地，虽然指数函数y＝a^x(a>1)与一次函数y＝kx(k>0)在区间[0，＋∞)上都单调递07(□)增，但它们的增长速度不同，随着x的增大，08(□)指数函数y＝a^x(a>1)的增长速度越来越快，即使09(□)k的值远远大于10(□)a的值，11(□)y＝a^x(a>1)的增长速度最终都会超过并远远大于12(□)y＝kx的增长速度．尽管在x的一定变化范围内，13(□)a^x会小于14(□)kx，但由于15(□)指数函数y＝a^x(a>1)的增长最终会快于16(□)一次函数y＝kx(k>0)的增长，因此，总会存在一个x₀，当x>x₀时，恒有17(□)a^x>18(□)kx.

(5)一般地，虽然对数函数y＝log_ax(a>1)与一次函数y＝kx(k>0)在区间(0，＋∞)上都单调递19(□)增，但它们的增长速度不同．随着x的增大，20(□)一次函数y＝kx(k>0)保持固定的增长速度，而21(□)对数函数y＝log_ax(a>1)的增长速度越来越慢．不论22(□)a的值比23(□)k的值大多少，在一定范围内，24(□)log_ax可能会大于25(□)kx，但由于26(□)log_ax的增长慢于27(□)kx的增长，因此总会存在一个x₀，当x>x₀时，恒有28(□)log_ax<29(□)kx.

【新知拓展】

指数函数、对数函数和幂函数的增长差异

一般地，在区间(0，＋∞)上，尽管函数y＝a^x(a＞1)，y＝log_ax(a＞1)和y＝xⁿ(n＞0)都是增函数，但它们的增长速度不同，而且不在同一个“档次”上．随着x的增大，y＝a^x(a＞1)的增长速度越来越快，会超过并远远大于y＝xⁿ(n＞0)的增长速度，而y＝log_ax(a＞1)的增长速度则会越来越慢，总会存在一个x₀，当x＞x₀时，就有log_ax＜xⁿ＜a^x.

1．判一判(正确的打“√”，错误的打“×”)

(1)函数y＝x²比y＝2^x增长的速度更快些．(　　)

(2)函数y＝kx＋b(k＞0)的增长特点是直线上升，其增长速度不变．(　　)

(3)对数函数y＝log_ax(a＞1)的增长特点是随自变量的增大，函数值增大的速度越来越慢．(　　)

答案　(1)×　(2)√　(3)√

2．做一做

(1)下图反映的是下列哪类函数的增长趋势(　　)

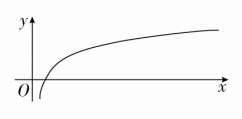
A．一次函数 B．幂函数

C．对数函数 D．指数函数

(2)当x越来越大时，下列函数中，增长速度最快的应该是(　　)

A．y＝100x B．y＝100ln x

C．y＝x¹⁰⁰ D．y＝100·2^x

(3)已知变量x，y满足y＝1－3x，当x增加1个单位时，y的变化情况是________．

答案　(1)C　(2)D　(3)减少3个单位

题型一  几类函数模型增长差异的比较

例1　四个变量y₁，y₂，y₃，y₄随变量x变化的数据如表：

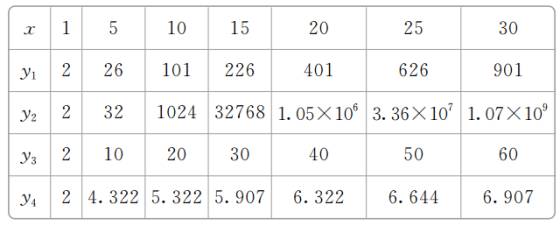
关于x呈指数函数变化的变量是________．

[解析]　以爆炸式增长的变量是呈指数函数变化的．从表格中可以看出，四个变量y₁，y₂，y₃，y₄均是从2开始变化，变量y₁，y₂，y₃，y₄都是越来越大，但是增长速度不同，其中变量y₂的增长速度最快，可知变量y₂关于x呈指数函数变化．

[答案]　y₂

金版点睛

常见的函数及增长特点

(1)线性函数

线性函数y＝kx＋b(k＞0)的增长特点是直线上升，其增长速度不变．

(2)指数函数

指数函数y＝a^x(a＞1)的增长特点是随着自变量的增大，函数值增大的速度越来越快，即增长速度急剧，形象地称为“指数爆炸”．

(3)对数函数

对数函数y＝log_ax(a＞1)的增长特点是随着自变量的增大，函数值增大的速度越来越慢，即增长速度平缓．

(4)幂函数

幂函数y＝xⁿ(n＞0)的增长速度介于指数增长和对数增长之间．

　有一组数据如下表：

现准备用下列函数中的一个近似地表示这些数据满足的规律，其中最接近的一个是(　　)

A．v＝log₂t B．v＝log12t

C．v＝2(t2－1) D．v＝2t－2

答案　C

解析　从表格中看到此函数为单调增函数，排除B；增长速度越来越快，排除A，D，选C．

题型二  指数函数、对数函数与幂函数的比较

例2　函数f(x)＝2^x和g(x)＝x³的图象如图所示．设两函数的图象交于点A(x₁，y₁)，B(x₂，y₂)，且x₁<x₂.

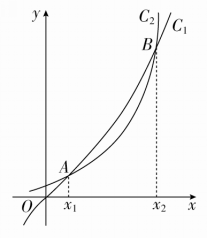
(1)请指出图中曲线C₁，C₂分别对应的函数；

(2)结合函数图象，判断f(6)，g(6)，f(2018)，g(2018)的大小．

[解]　(1)当x充分大时，图象位于上方的函数是指数函数y＝2^x，另一个函数就是幂函数y＝x³.

∴C₁对应的函数为g(x)＝x³，C₂对应的函数为f(x)＝2^x.

(2)∵f(1)>g(1)，f(2)<g(2)，f(9)<g(9)，f(10)>g(10)，

∴1<x₁<2,9<x₂<10.

∴x₁<6<x_2,2018>x₂.

从图象上可以看出，当x₁<x<x₂时，f(x)<g(x)，

∴f(6)<g(6)．

当x>x₂时，f(x)>g(x)，∴f(2018)>g(2018)．

又g(2018)>g(6)，

∴f(2018)>g(2018)>g(6)>f(6)．

金版点睛

由图象判断指数函数、对数函数和幂函数的方法

根据图象判断增长型的指数函数、对数函数和幂函数时，通常是观察函数图象上升得快慢，即随着自变量的增大，图象最“陡”的函数是指数函数；图象趋于平缓的函数是对数函数．

　函数f(x)＝1.1^x，g(x)＝ln x＋1，h(x)＝x2(1)2(1)的图象如图所示，试分别指出各曲线对应的函数，并比较三个函数的增长差异(以1，a，b，c，d，e为分界点)．

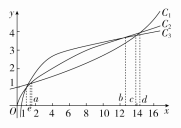
解　由指数爆炸、对数增长、幂函数增长的差异可得曲线C₁对应的函数是f(x)＝1.1^x，

曲线C₂对应的函数是h(x)＝x2(1)2(1)，曲线C₃对应的函数是g(x)＝ln x＋1.

由题图知，

当x<1时，f(x)>h(x)>g(x)；

当1<x<e时，f(x)>g(x)>h(x)；

当e<x<a时，g(x)>f(x)>h(x)；

当a<x<b时，g(x)>h(x)>f(x)；

当b<x<c时，h(x)>g(x)>f(x)；

当c<x<d时，h(x)>f(x)>g(x)；

当x>d时，f(x)＞h(x)>g(x)．

1．下列函数中，随着x的增大，增长速度最快的是(　　)

A．y＝50 B．y＝1000x

C．y＝0.4·2^x－1 D．y＝1000(1)e^x

答案　D

解析　指数函数y＝a^x，在a＞1时呈爆炸式增长，而且a越大，增长速度越快，选D．

2．有一组实验数据如下表所示：

下列所给函数较适合的是(　　)

A．y＝log_ax(a＞1) B．y＝ax＋b(a＞1)

C．y＝ax²＋b(a＞0) D．y＝log_ax＋b(a＞1)

答案　C

解析　通过所给数据可知y随x增大，其增长速度越来越快，而A，D中的函数增长速度越来越慢，而B中的函数增长速度保持不变，故选C．

3．当2<x<4时，2^x，x²，log₂x的大小关系是(　　)

A．2^x＞x²＞log₂x B．x²＞2^x＞log₂x

C．2^x＞log₂x＞x² D．x²＞log₂x＞2^x

答案　B

解析　解法一：在同一平面直角坐标系中画出函数y＝log₂x，y＝x²和y＝2^x的图象(图略)，在区间(2,4)内从上往下依次是y＝x²，y＝2^x，y＝log₂x的图象，所以x²>2^x>log₂x.

解法二：比较三个函数值的大小，作为选择题，可以采用特殊值代入法，如取x＝3，经检验易知选B．

4．已知某工厂生产某种产品的月产量y与月份x满足关系y＝a·(0.5)^x＋b，现已知该厂今年1月、2月生产该产品分别为1万件、1.5万件，则此厂3月份该产品的产量为________万件．

答案　1.75

解析　∵y＝a·(0.5)^x＋b，且当x＝1时，y＝1，当x＝2时，y＝1.5，则有1.5＝a×0.25＋b，(1＝a×0.5＋b，)解得b＝2.(a＝－2，)

∴y＝－2×(0.5)^x＋2.

当x＝3时，y＝－2×0.125＋2＝1.75(万件)．

5．下面是四个不同函数随x的增大而得到的函数值表：

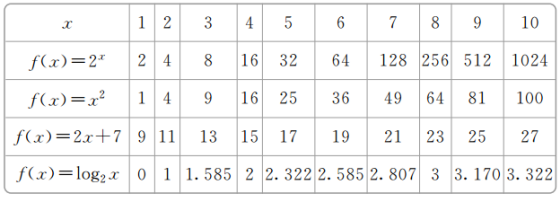
试问：

(1)随着x的增大，各函数的函数值有什么共同的变化趋势？

(2)各函数增长速度的快慢有什么不同？

解　(1)随着x的增大，各函数的函数值都在增大．

(2)由题表可以看出：各函数增长速度的快慢不同，其中f(x)＝2^x的增长速度最快，而且越来越快；其次为f(x)＝x²，增长速度也在变大；而f(x)＝2x＋7的增长速度不变；增长速度最慢的是f(x)＝log₂x，其增长速度越来越小．