第2课时　建立函数模型解决实际问题

(教师独具内容)

课程标准：结合现实情境中的具体问题，会选择合适的函数模型来解决问题．

教学重点：建立函数模型解决实际问题．

教学难点：建立函数模型．

 

【知识导学】

知识点一　　　用函数模型解决实际问题的步骤

(1)01(□)审题：弄清题意，分清条件和结论，理顺数量关系，用函数刻画实际问题，初步选择模型．

(2)02(□)建模：将文字语言转化为数学语言，利用数学知识，建立相应的函数模型．

(3)03(□)求模：求解函数模型，得到数学结论．

(4)04(□)还原：利用数学知识和方法得出的结论还原到实际问题中．

可将这些步骤用框图表示如下：

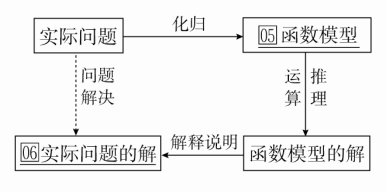
知识点二　　　数据拟合

(1)定义：通过一些数据寻求事物规律，往往是通过绘出这些数据在直角坐标系中的点，观察这些点的整体特征，看它们接近我们熟悉的哪一种函数图象，选定函数形式后，将一些数据代入这个函数的一般表达式，求出具体的函数表达式，再做必要的检验，基本符合实际，就可以确定这个函数基本反映了事物规律，这种方法称为数据拟合．

(2)数据拟合的步骤

①以所给数据作为点的坐标，在平面直角坐标系中绘出各点；

②依据点的整体特征，猜测这些点所满足的函数形式，设其一般形式；

③取特殊数据代入，求出函数的具体解析式；

④做必要的检验．

【新知拓展】

1．常见的函数模型

 

2．分段函数模型：y＝()()gx，x∈I2.(fx，x∈I1，)

1．判一判(正确的打“√”，错误的打“×”)

(1)能用指数型函数f(x)＝abx＋c(a，b，c为常数，a>0，b>1)表达的函数模型，称为指数型函数模型，也常称为“爆炸型”函数．(　　)

(2)函数y＝2(1)·3x＋1属于幂函数模型．(　　)

(3)当a＞1，n＞0时，在区间(0，＋∞)上，对任意的x，总有logax＜xn＜ax成立．(　　)

(4)当x>100时，函数y＝10x－1比y＝lg x增长的速度快．(　　)

答案　(1)√　(2)×　(3)×　(4)√

　 　　　　　　　　　　　　　　　　　　

 

2．做一做

(1)某种植物生长发育的数量y与时间x的关系如下表：

 

 

则下面的函数关系式中，拟合效果最好的是(　　)

A．y＝2x－1 B．y＝x2－1

C．y＝2x－1 D．y＝1.5x2－2.5x＋2

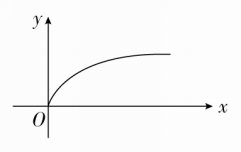
(2)如图所示的曲线反映的是________函数模型的增长趋势．

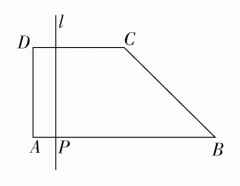
(3)已知直角梯形ABCD如图所示，CD＝2，AB＝4，AD＝2，线段AB上有一点P，过点P作AB的垂线l，当点P从点A运动到点B时，记AP＝x，l截直角梯形的左边部分面积为y，则y关于x的函数关系式为________．

答案　(1)D　(2)对数

(3)y＝()x－42＋6，2<x≤4(1)

题型一  函数模型的选择问题

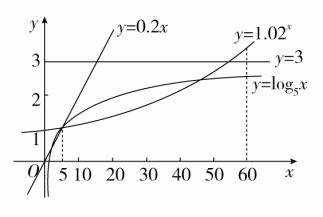
例1　某学校为了实现60万元的生源利润目标，准备制定一个激励招生人员的奖励方案：在生源利润达到5万元时，按生源利润进行奖励，且奖金y(单位：万元)随生源利润x(单位：万元)的增加而增加，但奖金总数不超过3万元，同时奖金不超过利润的20%.现有三个奖励模型：y＝0.2x，y＝log5x，y＝1.02x，其中哪个模型符合该校的要求？

[解]　借助工具作出函数y＝3，y＝0.2x，y＝log5x，y＝1.02x的图象(如图所示)，观察图象可知，在区间[5,60]上，y＝0.2x，y＝1.02x的图象都有一部分在直线y＝3的上方，只有y＝log5x的图象始终在y＝3和y＝0.2x的下方，这说明只有按模型y＝log5x进行奖励才符合学校的要求．

金版点睛

不同函数模型的选取标准

(1)线性函数增长模型适合于描述增长速度不变的变化规律；

(2)指数函数增长模型适合于描述增长速度急剧的变化规律；

(3)对数函数增长模型适合于描述增长速度平缓的变化规律；

(4)幂函数增长模型适合于描述增长速度一般的变化规律．

因此，需抓住题中蕴含的数学信息，恰当、准确地建立相应变化规律的函数模型来解决实际问题．

 

　据调查：人类在能源利用与森林砍伐中使CO2浓度增加．据测，2015年、2016年、2017年大气中的CO2浓度分别比2014年增加了1个单位，3个单位，6个单位．若用一个函数模型每年CO2浓度增加的单位数y与年份增加数x的关系，模拟函数可选用二次函数f(x)＝px2＋qx＋r(其中p，q，r为常数)或函数g(x)＝a·bx＋c(其中a，b，c为常数)，又知2018年大气中的CO2浓度比2014年增加了16.5个单位，请问用以上哪个函数作模拟函数较好？

解　若以f(x)＝px2＋qx＋r作模拟函数，

则依题意，得9p＋3q＋r＝6，(4p＋2q＋r＝3，)解得r＝0.(，)

∴f(x)＝2(1)x2＋2(1)x.

若以g(x)＝a·bx＋c作模拟函数，

则ab3＋c＝6.(ab2＋c＝3，)解得c＝－3.(，)

∴g(x)＝3(8)·2(3)x－3.

利用f(x)，g(x)对2018年CO2浓度作估算，

则其数值分别为f(4)＝10单位，g(4)＝10.5单位，

∵|f(4)－16.5|>|g(4)－16.5|，

故g(x)＝3(8)·2(3)x－3作模拟函数与2018年的实际数据较为接近，用g(x)＝3(8)·2(3)x－3作模拟函数较好.

 

题型二  建立函数模型解决实际问题

例2　某工厂生产某种产品，每件产品的出厂价为50元，其成本价为25元，因为在生产过程中平均每生产一件产品有0.5立方米污水排出，为了净化环境，工厂设计了两套方案对污水进行处理，并准备实施．

方案一：工厂的污水先净化处理后再排出，每处理1立方米污水所用原料费为2元，并且每月排污设备损耗费为30000元；

方案二：工厂将污水排到污水处理厂统一处理，每处理1立方米污水需付14元的排污费，问：

(1)工厂每月生产3000件产品时，你作为厂长，在不污染环境，又节约资金的前提下应选择哪种方案？通过计算加以说明；

(2)若工厂每月生产6000件产品，你作为厂长，又该如何决策呢？

[解]　设工厂每月生产x件产品时，选择方案一的利润为y1，选择方案二的利润为y2，由题意知

y1＝(50－25)x－2×0.5x－30000＝24x－30000.

y2＝(50－25)x－14×0.5x＝18x.

(1)当x＝3000时，y1＝42000，y2＝54000，

∵y1<y2，∴应选择方案二处理污水．

(2)当x＝6000时，y1＝114000，y2＝108000，

∵y1>y2，∴应选择方案一处理污水．

金版点睛

建立函数模型是为了预测和决策，预测准不准主要看建立的函数模型与实际的拟合程度.而要获得好的拟合度，就需要丰富、详实的数据.

 

 

　某公司预投资100万元，有两种投资可供选择：

甲方案年利率10%，按单利计算，5年后收回本金和利息；

乙方案年利率9%，按每年复利一次计算，5年后收回本金和利息．

哪种投资更有利？这种投资比另一种投资5年可多得利息多少万元？(结果精确到0.01万元)

解　按甲方案，每年利息100×10%＝10,5年后本息合计150万元；

按乙方案，第一年本息合计100×1.09，第二年本息合计100×1.092，…，5年后本息合计100×1.095≈153.86万元．

故按乙方案投资5年可多得利息3.86万元，更有利.

题型三  用分段函数模型解决实际问题

例3　提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度v(单位：千米/小时)是车流密度x(单位：辆/千米)的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：当20≤x≤200时，车流速度v是车流密度x的一次函数．

(1)当0≤x≤200时，求函数v(x)的表达式；

(2)车流密度x为多大时，车流量(单位时间内通过桥上某观测点的车辆数，单位：辆/小时)f(x)＝x·v(x)可以达到最大，并求出最大值．(精确到1辆/小时)

[解]　(1)由题意，当0≤x≤20时，v(x)＝60；

当20≤x≤200时，设v(x)＝ax＋b，

由已知得20a＋b＝60，(200a＋b＝0，)解得.(200)

故函数v(x)的表达式为

v(x)＝()200－x，20<x≤200.(1)

(2)依题意并结合(1)可得

f(x)＝()x200－x，20<x≤200.(1)

当0≤x≤20时，f(x)为增函数，故当x＝20时，f(x)在区间[0,20]上取得最大值60×20＝1200；

当20<x≤200时，f(x)＝3(1)x(200－x)＝－3(1)(x－100)2＋3(10000)≤3(10000)，当且仅当x＝100时，等号成立．

所以当x＝100时，f(x)在区间(20,200]上取得最大值3(10000).

综上可得，当x＝100时，f(x)在区间[0,200]上取得最大值3(10000)≈3333.

即当车流密度为100辆/千米时，车流量可以达到最大，最大值约为3333辆/小时．

金版点睛

解决分段函数问题需注意的几个问题

(1)所有分段的区间的并集就是分段函数的定义域．

(2)求分段函数的函数值时，先要弄清自变量在哪个区间内取值，然后再用该区间上的解析式来计算函数值．

(3)求分段函数的最值时，先求函数在每一段范围内的最值，然后比较这几个最值的大小，最后求出分段函数的最值．

 

 

 

　为了预防流感，某学校对教室用过氧乙酸熏蒸进行消毒．已知药物在释放过程中，室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比，药物释放完毕后，y与t的函数关系式为y＝16(1)t－a(a为常数)，如图所示．

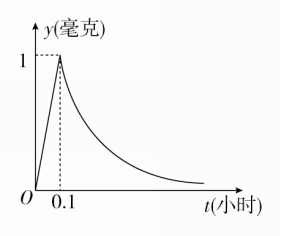
(1)从药物释放开始，写出y与t的函数关系式；

(2)据测定，当教室空气中的含药量降低到每立方米0.25毫克以下时，学生可进教室，问这次消毒多久后学生才能回到教室．

解　(1)由图象可知，当0≤t≤0.1时，y＝10t；

当t＝0.1时，由1＝16(1)0.1－a，得a＝0.1，

∴当t>0.1时，y＝16(1)t－0.1.

∴y＝t－0.1，t>0.1.(1)

(2)由题意可知，16(1)t－0.1<0.25，解得t>0.6，即这次消毒0.6×60＝36(分钟)后，学生才能进教室.

题型四  建立拟合函数模型解决实际问题

例4　18世纪70年代，德国科学家提丢斯发现金星、地球、火星、木星、土星离太阳的平均距离(天文单位)如下表：

 

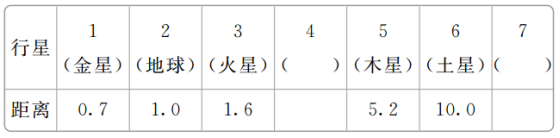
他研究行星排列规律后预测在火星与木星之间应该有一颗大的行星，后来果然发现了谷神星，但不算大行星，它可能是一颗大行星爆炸后的产物，请你推测谷神星的位置，在土星外面的行星与太阳的距离大约是多少？

[解]　由数值对应表作散点图如图．

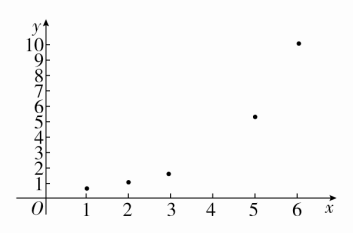
由图采用指数型函数作模型，设f(x)＝a·bx＋C．

代入(1,0.7)，(2,1.0)，(3,1.6)得ab3＋c＝1.6，③(ab2＋c＝1.0，②)

(③－②)÷(②－①)得b＝2，代入①②，

得4a＋c＝1.0，(2a＋c＝0.7，)解得，(2)∴f(x)＝20(3)·2x＋5(2).

∵f(5)＝5(26)＝5.2，f(6)＝10，

∴符合对应表值，∴f(4)＝2.8，f(7)＝19.6，

所以谷神星大约在离太阳2.8天文单位处．在土星外面的行星与太阳的距离大约是19.6天文单位．

金版点睛

对于此类实际应用问题，关键是建立适当的函数关系式，再解决数学问题，最后验证并结合问题的实际意义作出回答，这个过程就是先拟合函数再利用函数解题．函数拟合与预测的一般步骤是：

(1)能够根据原始数据、表格，绘出散点图．

(2)通过考察散点图，画出“最贴近”的直线或曲线，即拟合直线或拟合曲线．如果所有实际点都落到了拟合直线或曲线上，滴“点”不漏，那么这将是个十分完美的事情，但在实际应用中，这种情况一般不会发生．因此，使实际点尽可能均匀分布在直线或曲线两侧，使两侧的点数大体相等，得出的拟合直线或拟合曲线就是“最贴近”的了．

(3)根据所学函数知识，求出拟合直线或拟合曲线的函数关系式．

(4)利用函数关系式，根据条件对所给问题进行预测和控制，为决策和管理提供依据．

 

 

 

　某商场经营一批进价是每件30元的商品，在市场销售中发现，此商品的销售单价x元与日销售量y件之间有如下关系(见下表)：

 

(1)在所给的坐标系中，根据表中提供的数据描出实数对(x，y)对应的点，并确定y与x的一个函数关系式y＝f(x)；

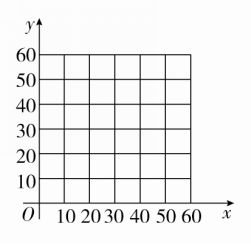
(2)设经营此商品的日销售利润为P元，根据上述关系式写出P关于x的函数关系式，并指出销售单价x为多少元时，才能获得最大日销售利润？

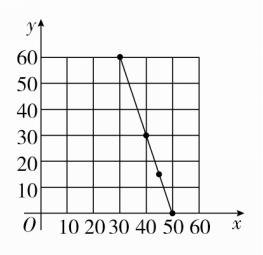
解　(1)根据题干中所给表作图，如图，点(30,60)，(40,30)，(45,15)，(50,0)在同一条直线上，设此直线为y＝kx＋b，

∴45k＋b＝15(50k＋b＝0，)⇒b＝150.(k＝－3，)

∴y＝－3x＋150(x∈N，x≤50)，

经检验点(30,60)，(40,30)也在此直线上，故所求函数关系式为y＝－3x＋150(x∈N，x≤50)．

(2)依题意有P＝y(x－30)＝(－3x＋150)(x－30)

＝－3(x－40)2＋300，

∴当x＝40时，P有最大值300.

故销售单价为40元时，才能获得最大日销售利润．

 

1．四个物体同时从某一点出发向前运动，其路程fi(x)(i＝1,2,3,4)关于时间x(x>1)的函数关系是f1(x)＝x2，f2(x)＝2x，f3(x)＝log2x，f4(x)＝2x.如果它们一直运动下去，最终在最前面的物体具有的函数关系是(　　)

A．f1(x)＝x2 B．f2(x)＝2x

C．f3(x)＝log2x D．f4(x)＝2x

答案　D

解析　由增长速度可知，当自变量充分大时，指数函数的值最大，故选D．

2．某种动物繁殖数量y(只)与时间x(年)的关系为y＝alog2(x＋1)，设这种动物第一年有100只，到第7年它们发展到(　　)

A．300只 B．400只

C．500只 D．600只

答案　A

解析　由已知第一年有100只，得a＝100.将a＝100，x＝7代入y＝alog2(x＋1)，得y＝300.

3．某同学最近5年内的学习费用y(千元)与时间x(年)的关系如图所示，则可选择的模拟函数模型是(　　)

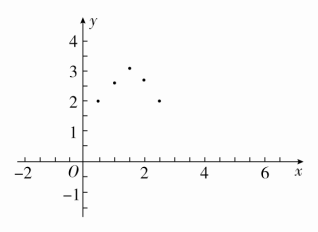
A．y＝ax＋b B．y＝ax2＋bx＋c

C．y＝aex＋b D．y＝aln x＋b

答案　B

解析　二次函数模型的表达式为y＝ax2＋bx＋c(a，b，c为常数，a≠0)，其函数图象与题图中的图形相符，因此可选择的模拟函数模型为二次函数模型．故选B．

4.如图所示，由桶1向桶2倒水，开始时，桶1中有a L水，桶2中无水，t分钟后，桶1中剩余水为y1 L，满足函数关系式y1＝ae－nt，假设经过5分钟，桶1和桶2中的水一样多，则再过________分钟，桶1中的水只有8(a) L.

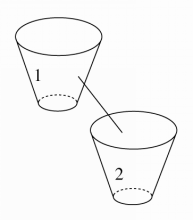
答案　10

解析　由题意，可得ae－5n＝2(a)，n＝5(1)ln 2，令ae－5(1)tln 2＝8(a)，解得t＝15，从而再经过10分钟，桶1中的水只有8(a) L.

5．医院通过撒某种药物对病房进行消毒．已知开始撒放这种药物时，浓度激增，中间有一段时间，药物的浓度保持在一个理想状态，随后药物浓度开始下降．若撒放药物后3小时内的浓度变化可用下面的函数表示，其中x表示时间(单位：小时)，f(x)表示药物的浓度：

f(x)＝()()()－3x＋492<x≤3.(431<x≤2，)

(1)撒放药物多少小时后，药物的浓度最高？能维持多长时间？

(2)若需要药物浓度在41.75以上消毒1.5小时，那么在撒放药物后，能否达到消毒要求？并简要说明理由．

解　(1)当0<x≤1时，f(x)＝－x2＋4x＋40＝－(x－2)2＋44，

∴f(x)在(0,1]上单调递增，其最大值为f(1)＝43；

f(x)在(2,3]上单调递减，故当2<x≤3时，f(x)<－3×2＋49＝43.

因此，撒放药物1小时后，药物的浓度最高为43，并维持1小时．

(2)当0<x≤1时，令f(x)＝41.75，即－(x－2)2＋44＝41.75，解得x＝3.5(舍去)或x＝0.5；

当2<x≤3时，令f(x)＝41.75，即－3x＋49＝41.75，解得x≈2.42.

因此药物浓度在41.75以上的时间约为2.42－0.5＝1.92小时，

∴撒放药物后，能够达到消毒要求．