5.1.2　弧度制

(教师独具内容)

课程标准：了解弧度制的概念，能进行弧度与角度的互化，体会引入弧度制的必要性．

教学重点：1.弧度制的意义.2.角度与弧度的互化.3.弧度制下，弧长和扇形面积公式的运用．

教学难点：弧度制的概念及角度与弧度的互化.

【知识导学】

知识点一　　　角的单位制

(1)用01(□)度作为单位来度量角的单位制叫做角度制，规定1度的角等于周角的360(1).

(2)长度等于02(□)半径长的圆弧所对的03(□)圆心角叫做1弧度的角，弧度单位用符号rad表示，读作04(□)弧度，通常略去不写．以05(□)弧度作为单位来度量角的单位制叫做弧度制．

(3)弧度数的计算

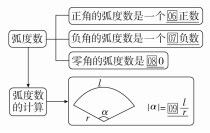
知识点二　　　角度与弧度的换算

(1)角度制与弧度制的换算

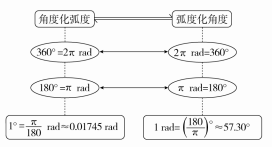
(2)一些特殊角的度数与弧度数的对应表

知识点三　　　扇形的弧长及面积公式

设扇形的半径为r，弧长为l，α(0<α<2π)为其圆心角的弧度数，n为圆心角的角度数，则扇形的弧长：l＝180(nπr)＝01(□)αr，扇形的面积：S＝360(nπr2)＝02(□)2(1)lr＝2(1)α·r².

【新知拓展】

(1)无论是以“度”还是以“弧度”为单位，角的大小都是一个与“半径”大小无关的定值，仅仅是为了能使概念描述更具体的一个“过渡量”而已．

(2)用弧度为单位表示角的大小时，“弧度”两字可以省略不写，如sin2是指sin(2弧度)，π＝180°是指π弧度＝180°；但如果以度为单位表示角时，度就不能省去．

(3)用弧度为单位表示角时，常常把弧度数写成多少π的形式，如无特殊要求，不必把π写成小数，如45°＝4(π)弧度，不必写成45°≈0.785弧度．

(4)角度制和弧度制表示的角不能混用．如α＝2kπ＋30°，k∈Z；β＝k·90°＋4(π)，k∈Z，都不正确．

(5)弧度制是十进制，而角度制是六十进制．

1．判一判(正确的打“√”，错误的打“×”)

(1)大圆中1弧度角比小圆中1弧度角大．(　　)

(2)圆心角为1弧度的扇形的弧长都相等．(　　)

(3)用弧度表示的角都是正角．(　　)

(4)“度”和“弧度”是度量角的两种不同的度量单位．(　　)

答案　(1)×　(2)×　(3)×　(4)√

2．做一做

(1)在半径为5 cm的圆中，圆心角为周角的3(2)的角所对的圆弧长为(　　)

A.3(4π) cm   B.3(20π) cm

C.3(10π) cm   D.3(50π) cm

(2)－135°化为弧度为________，3(11π)化为角度为________．

答案　(1)B　(2)－4(3π)　660°

题型一  弧度制的概念

例1　下列命题中，假命题是(　　)

A．“度”与“弧度”是度量角的两种不同的度量单位

B．一度的角是周角的360(1)，一弧度的角是周角的2π(1)

C．1弧度是长度等于半径长的圆弧所对的圆心角，它是角的一种度量单位

D．不论是用角度制还是用弧度制度量角，它们均与圆的半径长短有关

[解析]　根据角度和弧度的定义，可知无论是角度制还是弧度制，角的大小与圆的半径长短无关，而是与弧长与半径的比值有关，所以D是假命题．选项A，B，C均为真命题．

[答案]　D

金版点睛

角度制和弧度制的比较

(1)弧度制是以“弧度”为单位来度量角的单位制，而角度制是以“度”为单位来度量角的单位制．

(2)1弧度的角是指等于半径长的弧所对的圆心角，而1度的角是指圆周角的360(1)的角，大小显然不同．

(3)无论是以“弧度”还是以“度”为单位来度量角，角的大小都是一个与“半径”大小无关的值．

(4)用“度”作为单位度量角时，“度”(即“°”)不能省略，而用“弧度”作为单位度量角时，“弧度”二字或“rad”通常省略不写．但两者不能混用，即在同一表达式中不能出现两种度量方法．

　下列叙述中正确的是(　　)

A．1弧度是1度的圆心角所对的弧

B．1弧度是长度为半径的弧

C．1弧度是1度的弧与1度的角之和

D．大圆中1弧度的圆心角与小圆中1弧度的圆心角一样大

答案　D

解析　弧度是度量角的大小的一种单位，而不是长度的度量单位，1弧度是长度等于半径的圆弧所对圆心角的大小，与圆的半径无关，故选D.

题型二  角度和弧度的换算

例2　把下列各角用另一种度量制表示出来：112°30′；36°；－12(5π)；3.5.

[解]　112°30′＝2(225)×180(π)＝8(5π).

36°＝36×180(π)＝5(π).

－12(5π)＝－12(5π)×π(180)°＝－75°.

3．5＝3.5×π(180)°≈3.5×57.3°＝200.55°(或200°33′)．

金版点睛

用弧度制表示角时“弧度”二字可以省略不写，而用角度制表示角时要特别注意单位“°”不能丢，因为1°与1是完全不同的两个角.

　(1)－300°化为弧度是(　　)

A．－3(4π)  B．－3(5π)  C．－4(7π)  D．－6(7π)

(2)5(8π)化为度数是(　　)

A．278°  B．280°  C．288°  D．318°

答案　(1)B　(2)C

解析　(1)－300°＝－300×180(π)＝－3(5π).

(2)5(8π)＝5(8)×180°＝288°.

题型三  用弧度制表示角的集合

例3　已知角α＝2005°.

(1)将α改写成β＋2kπ(k∈Z,0≤β<2π)的形式，并指出α是第几象限的角；

(2)在[－5π，0)内找出与α终边相同的角．

[解]　(1)2005°＝2005×180(π) rad＝36(401π) rad

＝36(41π) rad，

又π<36(41π)<2(3π)，

∴角α与36(41π)终边相同，是第三象限的角．

(2)与α终边相同的角为2kπ＋36(41π)(k∈Z)，

由－5π≤2kπ＋36(41π)<0，k∈Z知k＝－1，－2，－3.

∴在[－5π，0)内与α终边相同的角是

－36(31π)，－36(103π)，－36(175π).

金版点睛

用弧度制表示终边相同的角2kπ＋α(k∈Z)时，其中2kπ是π的偶数倍，而不是整数倍，还要注意角度制与弧度制不能混用.

　(1)将－1125°表示成2kπ＋α，0≤α<2π，k∈Z的形式为________；

(2)用弧度表示终边落在阴影部分内(不包括边界)的角的集合．

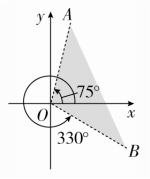
答案　(1)－8π＋4(7π)　(2)见解析

解析　(1)∵－1125°＝－180(π)＝－4(25π)，

∴－4(25π)＝－8π＋4(7π)，即－1125°＝－8π＋4(7π).

(2)因为终边落在OA处的角θ＝2kπ＋12(5π)，k∈Z，终边落在OB处的角θ＝2kπ－6(π)，k∈Z，所以终边落在阴影部分的角的集合为2kπ－6(π)<θ<2kπ＋12(5π)，k∈Z.

题型四  扇形的弧长及面积公式的应用

例4　(1)已知扇形的周长为8 cm，圆心角为2，则扇形的面积为________cm²；

(2)已知一半径为R的扇形，它的周长等于所在圆的周长，那么扇形的圆心角是多少弧度？面积是多少？

[解析]　(1)设扇形的半径为r cm，弧长为l cm，由圆心角为2 rad，依据弧长公式可得l＝2r，从而扇形的周长为l＋2r＝4r＝8，解得r＝2，则l＝4.

故扇形的面积S＝2(1)lr＝2(1)×4×2＝4(cm²)．

(2)设扇形的弧长为l，由题意得2πR＝2R＋l，所以l＝2(π－1)R，所以扇形的圆心角是R(l)＝2(π－1)，扇形的面积是2(1)lR＝(π－1)R².

[答案]　(1)4　(2)见解析

金版点睛

弧度制下涉及扇形问题的解题策略

(1)明确弧度制下扇形的面积公式是S＝2(1)lr＝2(1)|α|r²(其中l是扇形的弧长，r是扇形的半径，α(0<α<2π)是扇形的圆心角)．

(2)涉及扇形的周长、弧长、圆心角、面积等的计算，关键是先分析题目已知哪些量求哪些量，然后灵活运用弧长公式、扇形面积公式直接求解或列方程(组)求解．

已知扇形AOB的圆心角为120°，半径为6，求：

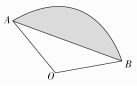
(1) ︵的长；

(2)扇形所含弓形的面积(即阴影面积)．

解　(1)∵120°＝3(2π)，∴︵的长l＝3(2π)×6＝4π.

(2)S_扇形AOB＝2(1)lr＝2(1)×4π×6＝12π.

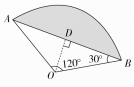
如图所示，过点O作OD⊥AB，交AB于D点，

于是有S_△OAB＝2(1)AB·OD＝2(1)×2×3×3＝9，

∴弓形的面积为S_扇形AOB－S_△AOB＝12π－9.

1．2145°转化为弧度数为(　　)

A.3(16)  B.2(32)  C.3(16π)  D.12(143π)

答案　D

解析　2145°＝2145×180(π) rad＝12(143π) rad.

2．α＝－2 rad，则α的终边在(　　)

A．第一象限   B．第二象限

C．第三象限   D．第四象限

答案　C

解析　∵1 rad≈57.30°，∴－2 rad≈－114.60°.故α的终边在第三象限．

3．在△ABC中，若A∶B∶C＝3∶5∶7，则角A，B，C的弧度数分别为________．

答案　5(π)，3(π)，15(7π)

解析　A∶B∶C＝3∶5∶7，则A占总度数的3＋5＋7(3)＝5(1)；B占总度数的3＋5＋7(5)＝3(1)；C占总度数的3＋5＋7(7)＝15(7).又三角形的内角和为π，则A为5(π)，B为3(π)，C为15(7π).

4．用弧度制表示终边落在第二象限的角的集合为________．

答案　<α<2kπ＋π，k∈Z(π)

解析　若角α的终边落在第二象限，则2kπ＋2(π)<α<2kπ＋π，k∈Z.

5．(1)把310°化成弧度；

(2)把12(5π) rad化成角度；

(3)已知α＝15°，β＝10(π)，γ＝1，θ＝105°，φ＝12(7π)，试比较α，β，γ，θ，φ的大小．

解　(1)310°＝180(π) rad×310＝18(31π) rad.

(2)12(5π) rad＝12(5π)°＝75°.

(3)解法一(化为弧度)：α＝15°＝15×180(π)＝12(π).θ＝105°＝105×180(π)＝12(7π).

显然12(π)<10(π)<1<12(7π)，故α<β<γ<θ＝φ.

解法二(化为角度)：β＝10(π)＝10(π)×π(180)°＝18°，γ＝1≈57.30°，φ＝12(7π)×π(180)°＝105°.

显然，15°<18°<57.30°<105°，故α<β<γ<θ＝φ.