5.2.1　三角函数的概念

(教师独具内容)

课程标准：1.借助单位圆理解三角函数(正弦、余弦、正切)的定义.2.掌握正弦、余弦、正切函数在各象限内的符号.3.理解终边相同的角的同一三角函数值相等．

教学重点：三角函数的定义；三角函数在各象限内的符号．

教学难点：任意角的三角函数的定义的建构过程.

【知识导学】

知识点一　　　三角函数的概念

(1)单位圆中三角函数的定义

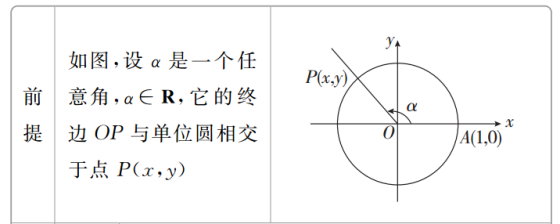
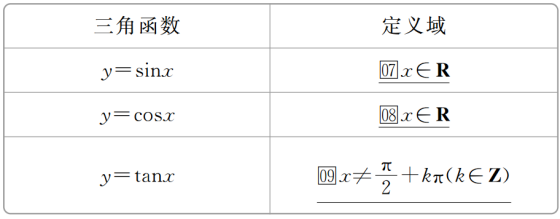
(2)三角函数的定义域

知识点二　三角函数值的符号

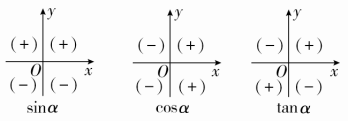
规律：一全正、二正弦、三正切、四余弦．

知识点三　诱导公式(一)

【新知拓展】

(1)三角函数值是比值，是一个实数，这个实数的大小与点P(x，y)在终边上的位置无关，只与角α的终边位置有关，即三角函数值的大小只与角有关．

(2)终边相同的角的同名三角函数值相等．

1．判一判(正确的打“√”，错误的打“×”)

(1)若α＝β＋720°，则cosα＝cosβ.(　　)

(2)若sinα＝sinβ，则α＝β.(　　)

(3)已知α是三角形的内角，则必有sinα>0.(　　)

答案　(1)√　(2)×　(3)√

2．做一做

(1)若sinα<0，且tanα<0，则α在(　　)

A．第一象限  B．第二象限

C．第三象限  D．第四象限

(2)若角α的终边经过点P(5，－12)，则sinα＝________，cosα＝________，tanα＝________.

(3)tan405°－sin450°＋cos750°＝________.

(4)sin2·cos3·tan4的值的符号为________．

答案　(1)D　(2)－13(12)　13(5)　－5(12)　(3)2(3)　(4)负

题型一  三角函数的定义

例1　已知角α的终边经过点P(－4a,3a)(a≠0)，求sinα，cosα，tanα的值．

[解]　r＝()()＝5|a|，

若a>0，则r＝5a，角α在第二象限，

sinα＝r(y)＝5a(3a)＝5(3)，cosα＝r(x)＝5a(－4a)＝－5(4)，

tanα＝x(y)＝－4a(3a)＝－4(3)；

若a<0，则r＝－5a，角α在第四象限，

sinα＝－5(3)，cosα＝5(4)，tanα＝－4(3).

[条件探究]　在本例中，若将题设条件改为：已知角α的终边在直线y＝x上，问题不变，怎样求解？

解　因为角α的终边在直线y＝x上，

所以可设P(a，a)(a≠0)为角α终边上任意一点．

则r＝ ()＝2|a|(a≠0)．

若a>0，则α为第一象限角，r＝2a，sinα＝2a(3a)＝2(3)，

cosα＝2a(a)＝2(1)，tanα＝a(3a)＝.

若a<0，则α为第三象限角，r＝－2a，sinα＝－2a(3a)＝－2(3)，cosα＝－2a(a)＝－2(1)，tanα＝a(3a)＝.

金版点睛

利用三角函数的定义求值的策略

(1)已知角α的终边在直线上求α的三角函数值时，常用的解题方法有以下两种：

方法一：先利用直线与单位圆相交，求出交点坐标，然后再利用正、余弦函数的定义求出相应三角函数值．

方法二：在α的终边上任选一点P(x，y)，P到原点的距离为r(r>0)．则sinα＝r(y)，cosα＝r(x).已知α的终边求α的三角函数值时，用这几个公式更方便．

(2)当角α的终边上点的坐标以参数形式给出时，要根据问题的实际情况对参数进行分类讨论．

(3)若终边在直线上时，因为角的终边是射线，应分两种情况处理．

　(1)设a<0，角α的终边与单位圆的交点为P(－3a,4a)，那么sinα＋2cosα的值等于(　　)

A.5(2)  B．－5(2)  C.5(1)  D．－5(1)

(2)已知角α终边上的点P(4,3m)，且sinα＝2(2)m，求m的值．

答案　(1)A　(2)见解析

解析　(1)∵点P在单位圆上，则|OP|＝1.

即()()＝1，解得a＝±5(1).

∵a<0，∴a＝－5(1)，

∴P点的坐标为5(4)，

∴sinα＝－5(4)，cosα＝5(3)，

∴sinα＋2cosα＝－5(4)＋2×5(3)＝5(2).

(2)∵P(4,3m)，∴r＝，

∴sinα＝r(y)＝16＋9m2(3m)＝2(2)m，

两边平方，得16＋9m2(9m2)＝2(1)m².

∴m²(9m²－2)＝0，∴m＝0或m＝±3(2).

题型二  三角函数值的符号　　　　　　　　　　　　　

例2　(1)若sinαtanα<0，且tanα(cosα)<0，则角α是(　　)

A．第一象限角   B．第二象限角

C．第三象限角   D．第四象限角

(2)判断下列各式的符号：

①tan120°·sin269°；②cos4·tan4(23π).

[解析]　(1)由sinαtanα<0可知sinα，tanα异号，

从而α为第二、三象限角．

由tanα(cosα)<0可知cosα，tanα异号，从而α为第三、四象限角．

综上可知，α为第三象限角．

(2)①∵120°是第二象限角，∴tan120°<0.

∵269°是第三象限角，∴sin269°<0，

∴tan120°·sin269°>0.

②∵π<4<2(3π)，∴4弧度是第三象限角，∴cos4<0.

∵－4(23π)＝－6π＋4(π)，

∴－4(23π)是第一象限角，∴tan4(23π)>0.

∴cos4·tan4(23π)<0.

[答案]　(1)C　(2)见解析

金版点睛

判断给定角的三角函数值正负的步骤

(1)确定α的终边所在的象限；

(2)利用三角函数值的符号规律，即“一全正、二正弦、三正切、四余弦”来判断．

　(1)若三角形的两内角A，B满足sinA·cosB<0，则此三角形必为(　　)

A．锐角三角形

B．钝角三角形

C．直角三角形

D．以上三种情况都有可能

(2)点P(tanα，cosα)在第三象限，则α是第________象限角．

答案　(1)B　(2)二

解析　(1)三角形内角的取值范围是(0，π)，故sinA>0.因为sinAcosB<0，所以cosB<0，所以B是钝角，故三角形是钝角三角形．

(2)因为点P(tanα，cosα)在第三象限，所以tanα<0，cosα<0，则角α的终边在第二象限.

题型三  与三角函数有关的定义域问题

例3　求下列函数的定义域：

(1)y＝tanx(sinx＋cosx)；

(2)y＝＋.

[解]　(1)要使函数有意义，需tanx≠0，

∴x≠kπ＋2(π)，且x≠kπ，k∈Z.

∴x≠2(kπ)，k∈Z.

于是函数的定义域是，k∈Z(kπ).

(2)要使函数有意义，需sinx≥0，(－cosx≥0，)

即()()2kπ≤x≤2kπ＋πk∈Z，(k∈Z，)

解得2kπ＋2(π)≤x≤2kπ＋π(k∈Z)，

∴函数的定义域是≤x≤2kπ＋π，k∈Z(π).

金版点睛

求解函数定义域的解题策略

(1)求函数的定义域，就是求使解析式有意义的自变量的取值范围，一般通过解不等式或不等式组求得，对于与三角函数有关的函数定义域问题，还要考虑三角函数自身定义域的限制．

(2)要特别注意求一个固定集合与一个含有无限多段的集合的交集时，可以取特殊值把不固定的集合写成若干个固定集合再求交集．

　求下列函数的定义域：

(1)y＝sinx＋tanx；

(2)y＝＋tanx.

解　(1)依题意，得()k∈Z，(π)

∴函数的定义域是，k∈Z(π).

(2)当sinx≥0且tanx有意义时，函数才有意义，

∴()2(π)(k∈Z)．

∴函数的定义域为x2kπ≤x<2kπ＋2(π)或2kπ＋2(π)<x≤2kπ＋π，k∈Z}. 

题型四   诱导公式(一)的应用

例4　计算：(1)sin6(11π)＋cos5(12π)tan4π；

(2)sin1140°cos(－690°)＋tan1845°.

[解]　(1)原式＝sin6(π)＋cos5(12π)tan0

＝sin6(π)＋0＝2(1).

(2)原式＝sin(3×360°＋60°)cos(－2×360°＋30°)＋tan(5×360°＋45°)

＝sin60°cos30°＋tan45°

＝2(3)×2(3)＋1＝4(7).

金版点睛

利用诱导公式化简的步骤

(1)将已知角化为k·360°＋α(k为整数，0°≤α<360°)或2kπ＋β(k为整数，0≤β<2π)的形式．

(2)将原三角函数值化为角α的同名三角函数值．

(3)借助特殊角的三角函数值或任意角的三角函数的定义达到化简求值的目的．

　求下列各式的值：

(1)cos3(25π)＋tan(－4(15π)))；

(2)sin810°＋tan1125°＋cos420°.

解　(1)原式＝cos3(π)＋tan4(π)

＝cos3(π)＋tan4(π)＝2(1)＋1＝2(3).

(2)原式＝sin(2×360°＋90°)＋tan(3×360°＋45°)＋cos(360°＋60°)＝sin90°＋tan45°＋cos60°＝1＋1＋2(1)＝2(5).

1．如果角α的终边过点P(2sin30°，－2cos30°)，则sinα的值等于(　　)

A.2(1)    B．－2(1)

C．－2(3)    D．－3(3)

答案　C

解析　由题意得P(1，－)，它与原点的距离r＝()＝2，所以sinα＝－2(3).

2．当α为第二象限角时，sinα(|sinα|)－|cosα|(cosα)的值是(　　)

A．1    B．0

C．2    D．－2

答案　C

解析　∵α为第二象限角，∴sinα>0，cosα<0，∴sinα(|sinα|)－|cosα|(cosα)＝sinα(sinα)－－cosα(cosα)＝2.

3．在△ABC中，若sinAcosBtanC<0，则△ABC是(　　)

A．锐角三角形    B．直角三角形

C．钝角三角形    D．锐角或钝角三角形

答案　C

解析　因为sinA>0，所以cosB，tanC中一定有一个小于0，即B，C中有一个钝角．

4．若750°角的终边上有一点(4，a)，则a＝________.

答案　3(3)

解析　tan750°＝tan(360°×2＋30°)＝tan30°＝3(3)＝4(a)，解得a＝3(3).

5．计算sin810°＋tan765°＋tan1125°＋cos360°.

解　原式＝sin(2×360°＋90°)＋tan(2×360°＋45°)＋tan(3×360°＋45°)＋cos(360°＋0°)

＝sin90°＋tan45°＋tan45°＋cos0°

＝1＋1＋1＋1＝4.