5.2.2　同角三角函数的基本关系

(教师独具内容)

课程标准：1.理解同角三角函数的基本关系式.2.会运用同角三角函数的基本关系式进行三角函数式的化简、求值和证明．

教学重点：同角三角函数关系式的推导及应用．

教学难点：同角三角函数基本关系式在解题中的逆用、变形应用及使用公式时由函数值正负号的选取而导致的角的范围的讨论.

【知识导学】

知识点一　　　同角三角函数的基本关系

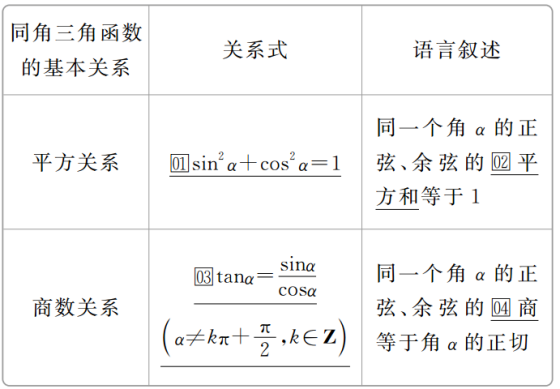
知识点二　　　同角三角函数的基本关系式的变形形式

(1)平方关系变形

sin²α＝01(□)1－cos²α，cos²α＝02(□)1－sin²α.

(2)商的变形

sinα＝03(□)tanαcosα，cosα＝tanα(sinα).

【新知拓展】

(1)同角三角函数的基本关系式揭示了“同角不同名”的三角函数的运算规律，这里“同角”有两层含义：一是“角相同”，二是对“任意”一个角(在使函数有意义的前提下)．关系式成立与角的表达形式无关，如sin²3α＋cos²3α＝1.

(2)sin²α是(sinα)²的简写，不能写成sinα².

(3)约定：教材中给出的三角恒等式，除特别注明的情况外，都是指两边都有意义情况下的恒等式．

1．判一判(正确的打“√”，错误的打“×”)

(1)由于平方关系对任意角都成立，则sin²α＋cos²β＝1也成立．(　　)

(2)同角三角函数的基本关系对任意角α都成立．(　　)

(3)当角α的终边与坐标轴重合时，sin²α＋cos²α＝1也成立．(　　)

(4)在利用平方关系求sinα或cosα时，会得到正负两个值．(　　)

答案　(1)×　(2)×　(3)√　(4)×

2．做一做

(1)若sinα＝5(4)，且α是第二象限角，则tanα的值等于(　　)

A．－3(4)  B.4(3)  C．±4(3)    D．±3(4)

(2)化简：＝________.

(3)已知3sinα＋5cosα(sinα－2cosα)＝－5，则tanα＝________.

答案　(1)A　(2)cos80°　(3)－16(23)

题型一  三角函数求值

例1　(1)已知cosα＝－5(4)，求sinα和tanα；

(2)已知tanα＝3，求3sinα＋5cosα(4sinα－cosα)的值．

[解]　(1)sin²α＝1－cos²α＝1－5(4)²＝5(3)²，

因为cosα＝－5(4)<0，所以α是第二或第三象限角，

当α是第二象限角时，sinα＝5(3)，tanα＝cosα(sinα)＝－4(3)；

当α是第三象限角时，sinα＝－5(3)，tanα＝cosα(sinα)＝4(3).

(2)解法一：原式＝3tanα＋5(4tanα－1)＝3×3＋5(4×3－1)＝14(11).

解法二：∵tanα＝3，∴sinα＝3cosα.

代入原式可得：原式＝3×3cosα＋5cosα(4×3cosα－cosα)＝14cosα(11cosα)＝14(11).

解法三：∵tanα＝3>0，∴sinα＝3cosα.

又sin²α＋cos²α＝1.∴sinα＝10(10)，cosα＝10(10)，

或sinα＝－10(10)，cosα＝－10(10)，

∴原式＝14(11).

[结论探究]　在本例(2)中条件不变的情况下，求4(3)sin²α＋2(1)cos²α的值．

解　原式＝sin2α＋cos2α(cos2α)

＝2()＝2()＝40(29).

金版点睛

1．求三角函数值的方法

(1)已知sinθ(或cosθ)求tanθ常用以下方式求解

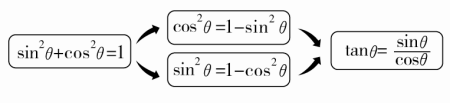
(2)已知tanθ求sinθ(或cosθ)常用以下方式求解

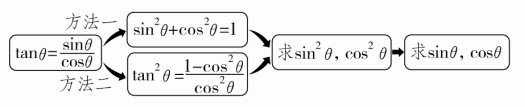
当角θ的范围不确定且涉及开方时，常因三角函数值的符号问题而对角θ分区间(象限)讨论．

2．已知角α的正切求关于sinα，cosα的齐次式的值的方法

(1)关于sinα，cosα的齐次式就是式子中的每一项都是关于sinα，cosα的式子且它们的次数之和相同，设为n次，将分子、分母同除以cosα的n次幂，其式子可化为关于tanα的式子，再代入求值．

(2)若无分母时，把分母看作1，并将1用sin²α＋cos²α来代换，将分子、分母同除以cos²α，可化为关于tanα的式子，再代入求值．

　(1)已知sinα＝13(12)，并且α是第二象限角，求cosα和tanα；

(2)已知sinα＋2cosα＝0，求2sinαcosα－cos²α的值；

(3)已知1＋2tanα(tan2α)＝3(1)，α∈，π(π)，求5cosα－sinα(sinα＋2cosα)的值．

解　(1)cos²α＝1－sin²α＝1－13(12)²＝13(5)²，

又α是第二象限角，所以cosα<0，cosα＝－13(5)，tanα＝cosα(sinα)＝－5(12).

(2)由sinα＋2cosα＝0，得tanα＝－2.

所以2sinαcosα－cos²α＝sin2α＋cos2α(2sinαcosα－cos2α)

＝tan2α＋1(2tanα－1)＝4＋1(－4－1)＝－1.

(3)∵1＋2tanα(tan2α)＝3(1)，∴3tan²α－2tanα－1＝0.

即(3tanα＋1)(tanα－1)＝0，

∴tanα＝－3(1)或tanα＝1.

∵α∈，π(π)，∴tanα<0，∴tanα＝－3(1)，

∴5cosα－sinα(sinα＋2cosα)＝5－tanα(tanα＋2)＝16(5).

题型二  sinα±cosα与sinαcosα关系的应用

例2　已知在△ABC中，sinA＋cosA＝5(1).

(1)求sinAcosA；

(2)判断△ABC是锐角三角形还是钝角三角形．

[解]　(1)∵sinA＋cosA＝5(1)，

∴两边平方，得1＋2sinAcosA＝25(1).

∴sinAcosA＝－25(12).

(2)由(1)sinAcosA＝－25(12)<0，且0<A<π，

可知cosA<0，∴A为钝角．

∴△ABC是钝角三角形．

金版点睛

三角函数求值中常见的变形公式

(1)sinα＋cosα，sinαcosα，sinα－cosα三个式子中，已知其中一个，可以求其他两个，即“知一求二”，它们的关系是：(sinα＋cosα)²＝1＋2sinαcosα；(sinα－cosα)²＝1－2sinαcosα.

(2)求sinα＋cosα或sinα－cosα的值，要根据α的范围注意判断它们的符号．

　已知0<θ<π，且sinθ－cosθ＝5(1)，求sinθ＋cosθ，tanθ的值．

解　∵sinθ－cosθ＝5(1)，

∴(sinθ－cosθ)²＝25(1)，

解得sinθcosθ＝25(12).

∵0<θ<π，且sinθcosθ＝25(12)>0，

∴sinθ>0，cosθ>0.

∴sinθ＋cosθ＝()＝

＝ 25(24)＝5(7).

由，(7)得，(3)

∴tanθ＝cosθ(sinθ)＝3(4).

题型三   三角函数式的化简与证明

例3　(1)化简：1－sin2130°(1－2sin130°cos130°) ；

(2)求证：tanα－sinα(tanαsinα)＝tanαsinα(tanα＋sinα).

[解]　(1)原式＝cos2130°(sin2130°－2sin130°cos130°＋cos2130°)

＝sin130°＋|cos130°|(|sin130°－cos130°|)＝sin130°－cos130°(sin130°－cos130°)＝1.

(2)证法一：∵右边＝()tanα－sinαtanαsinα(tan2α－sin2α)

＝()tanα－sinαtanαsinα(tan2α－tan2αcos2α)

＝()()tanα－sinαtanαsinα(tan2α1－cos2α)

＝()tanα－sinαtanαsinα(tan2αsin2α)

＝tanα－sinα(tanαsinα)＝左边，

∴原等式成立．

证法二：∵左边＝tanα－tanαcosα(tanαsinα)＝1－cosα(sinα)，

右边＝tanαsinα(tanα＋tanαcosα)＝sinα(1＋cosα)

＝()sinα1－cosα(1－cos2α)＝()sinα1－cosα(sin2α)＝1－cosα(sinα)，

∴左边＝右边，原等式成立．

[条件探究]　将本例(1)改为化简：1－sin2130°(1＋2sin130°cos130°).

解　原式＝()sin130°－|cos130°|(sin130°＋cos130°2)＝sin130°＋cos130°(sin130°＋cos130°)＝1.

金版点睛

1.利用同角三角函数关系化简的常用方法

(1)化切为弦，减少函数名称，便于约分化简；

(2)对含根号的，应先把被开方式化为完全平方，去掉根号，为防止出错，去掉根号后首先用绝对值符号表示，然后考虑正负；

(3)对含有高次的三角函数式，可借助于因式分解，或构造平方关系，以便于降幂化简.

2.简单的三角恒等式的证明思路

(1)从一边开始，证明它等于另一边；

(2)证明左、右两边等于同一个式子；

(3)逐步寻找等式成立的条件，达到由繁到简.

　化简：(1)1－cosα(sinα)·tanα＋sinα(tanα－sinα)；

(2) ()sin2θ(1).

解　(1)原式＝1－cosα(sinα)·＋sinα(sinα)

＝1－cosα(sinα)·1＋cosα(1－cosα)＝1－cosα(sinα)·()1－cos2α(1－cosα2)

＝1－cosα(sinα)·|sinα|(1－cosα)＝|sinα|(sinα)，

当sinα>0时，原式＝1；当sinα<0时，原式＝－1.

(2)原式＝·sin2θ(sinθ＋cosθ)

＝

＝＝1.

1．已知cosθ＝5(4)，且2(3π)<θ<2π，则tanθ(1)的值为(　　)

A.4(3)    B．－4(3)  

C.3(4)    D．－3(4)

答案　D

解析　由于cosθ＝5(4)，且2(3π)<θ<2π.

所以sinθ＝－＝－5(3)，

所以tanθ＝－4(3)，故tanθ(1)＝－3(4).

2．已知tanθ＝2，则sin²θ＋sinθcosθ－2cos²θ等于(　　)

A．－3(4)   B.4(5)  

C．－4(3)   D.5(4)

答案　D

解析　sin²θ＋sinθcosθ－2cos²θ

＝sin2θ＋cos2θ(sin2θ＋sinθcosθ－2cos2θ)＝tan2θ＋1(tan2θ＋tanθ－2)，

又tanθ＝2，故原式＝4＋1(4＋2－2)＝5(4).

3．若sinθ＝－5(4)，tanθ>0，则cosθ＝________.

答案　－5(3)

解析　∵sinθ<0，tanθ>0，∴θ在第三象限内，

∴cosθ＝－＝－5(3).

4．已知sinθ＝5(5)，则sin⁴θ－cos⁴θ的值为________．

答案　－5(3)

解析　由sinθ＝5(5)，可得cos²θ＝1－sin²θ＝5(4)，所以sin⁴θ－cos⁴θ＝(sin²θ＋cos²θ)(sin²θ－cos²θ)＝sin²θ－cos²θ＝5(1)－5(4)＝－5(3).

5．化简：cos2α－sin2α(1－2sinαcosα)·1－2sin2α(1＋2sinαcosα).

解　原式＝()cos2α－sin2α(sinα－cosα2)·()sin2α＋cos2α－2sin2α(sinα＋cosα2)

＝()()()cos2α－sin2αcos2α－sin2α(sin2α－cos2α2)＝1.