![]()

![]() 5.6.1 匀速圆周运动的数学模型
5.6.1 匀速圆周运动的数学模型
![]() 5.6.2 函数y=Asin(ωx+φ)的图象
5.6.2 函数y=Asin(ωx+φ)的图象
![]() (教师独具内容)
(教师独具内容)
课程标准:1.结合具体实例,了解y=Asin(ωx+φ)的实际意义.2.会用“五点法”画函数y=Asin(ωx+φ)的图象.3.能借助图象理解参数φ,ω,A的意义,了解参数的变化对函数图象的影响.4.掌握y=sinx与y=Asin(ωx+φ)图象间的变换关系,并能正确地指出其变换步骤.
教学重点:正确理解φ,ω,A对y=Asin(ωx+φ)的图象的影响,通过图象变换由y=sinx的图象得到y=Asin(ωx+φ)的图象.
教学难点:对图象变换与函数解析式变换的内在联系的理解.
![]()
【知识导学】
知识点一 参数A,ω,φ对函数y=Asin(ωx+φ)图象的影响
(1)φ对函数y=sin(x+φ),x∈R的图象的影响
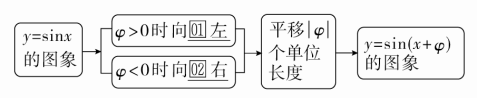
(2)ω(ω>0)对y=sin(ωx+φ)的图象的影响
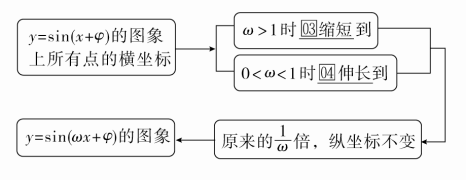
(3)A(A>0)对y=Asin(ωx+φ)的图象的影响
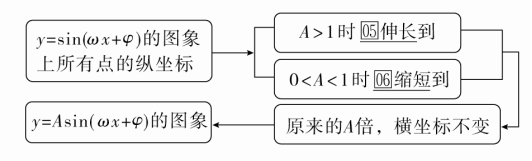
知识点二 由函数y=sinx的图象得到函数y=Asin(ωx+φ)的图象的途
径
由函数y=sinx的图象通过变换得到y=Asin(ωx+φ)的图象有两种主要途径:“01先平移后伸缩”与“02先伸缩后平移”.
(1)先平移后伸缩

(2)先伸缩后平移

知识点三 函数y=Asin(ωx+φ)(A>0,ω>0)的性质


注意隐含条件:
(1)两条相邻对称轴之间间隔为2个周期;
(2)函数在对称轴处取得最大值或最小值.
【新知拓展】
对于函数y=Asin(ωx+φ)(A>0,ω>0):
(1)A越大,函数的最大值越大,最大值与A是正比例关系.
(2)ω越大,函数的周期越小,ω越小,周期越大,周期与ω为反比例关系.
(3)φ大于0时,函数y=Asinωx的图象向左平移ω个单位长度得到函数y=Asin(ωx+φ)的图象,φ小于0时,函数y=Asinωx的图象向右平移ω个单位长度得到函数y=Asin(ωx+φ)的图象,即“加左减右”.
![]()
1.判一判(正确的打“√”,错误的打“×”)
(1)把y=sin2x的图象向左平移6个单位长度,得到
y=sin6.( )
(2)函数y=2sin4,x∈R的最大值为2.( )
(3)函数y=2sin4,x∈R的图象的一个对称中心为,0.( )
(4)五点法作函数y=2sin3在一个周期上的简图时,第一个点为,0.( )
答案 (1)× (2)√ (3)√ (4)×
2.做一做
(1)将函数y=sinx的图象向左平移3个单位长度后所得图象的解析式为( )
A.y=sinx-3 B.y=sinx+3
C.y=sin3 D.y=sin3
(2)要得到函数y=sin3的图象,只要将函数y=sin2x的图象( )
A.向左平移3个单位长度
B.向右平移3个单位长度
C.向左平移6个单位长度
D.向右平移6个单位长度
(3)将函数y=sinx的图象上所有点的横坐标缩短到原来的4倍(纵坐标不变)得到________的图象.
答案 (1)D (2)C (3)y=sin4x
![]()
题型一 作函数y=Asin(ωx+φ)的图象
例1 已知函数y=2sin3,用“五点法”画出其简图.
[解] 列表:
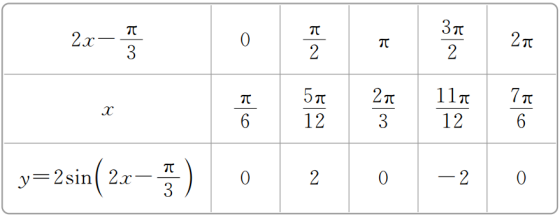
描点,连线得函数y=2sin3在一个周期内的图象.
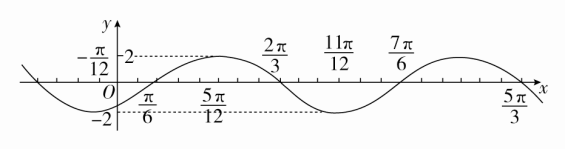
再将这部分图象向左或向右延伸kπ(k∈Z)个单位长度,就可得函数y=2sin3(x∈R)的图象.
金版点睛
用“五点法”作函数y=Asin(ωx+φ)图象的步骤
第一步:列表.
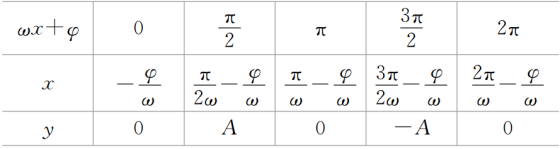
第二步:在同一坐标系中描出各点.
第三步:用光滑曲线连接这些点,得到一个周期内的图象.
作出函数y=2cos3在一个周期内的图象.
解 列表:
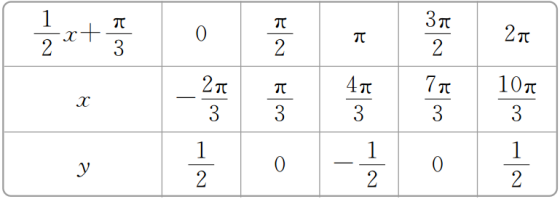
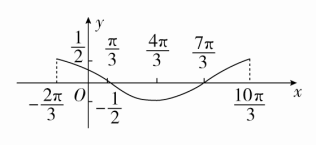
描点,连线得函数
y=2cos3在一个周期内的图象,如图.
题型二 函数的图象变换
例2 说明y=-2sin6+1的图象是由y=sinx的图象经过怎样变换得到的.
[解] 解法一(先伸缩后平移):


[条件探究] 将本例改为:y=2sin6+1的图象是由y=sinx的图象经过怎样的变换得到的?


金版点睛
三角函数图象变换的两种方法及两个注意
(1)两种方法:方法一是先平移,后伸缩;方法二是先伸缩,后平移.
(2)两个注意:
①两种变换中平移的单位长度不同,分别是|φ|和ω,但平移方向是一致的.
②虽然两种平移的单位长度不同,但因平移时平移的对象已有变化,所以得到的结果是一致的.
函数y=sin2的图象向右平移4个单位长度,再把所得图象上各点的横坐标缩短为原来的2,所得图象的函数解析式为________.
答案 y=sin4
解析 将原函数的图象向右平移4个单位长度,得到y=sin2=sin4的图象,再将所得图象上各点的横坐标缩短为原来的2,纵坐标不变,得到函数y=sin4的图象.
题型三 求三角函数的解析式
例3 如图是函数y=Asin(ωx+φ)2的图象的一部分,求此函数的解析式.
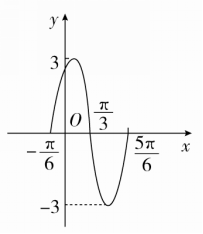
[解] 解法一(逐一定参法):
由图象知A=3,
T=6-6=π,
∴ω=T=2,∴y=3sin(2x+φ).
∵点,0在函数图象上,
∴0=3sin×2+φ,
∴-6×2+φ=kπ(k∈Z),得φ=3+kπ(k∈Z).
∵|φ|<2,∴φ=3,∴y=3sin3.
解法二(待定系数法):
由图象知A=3.
由图象过点,0和,0,且在,0处下降,在,0处上升,
可令+φ=2π,解得.
∴y=3sin3.
解法三(图象变换法):
由A=3,T=π,点,0在图象上,可知函数图象由y=3sin2x向左平移6个单位长度而得,
所以y=3sin6,即y=3sin3.
金版点睛
求函数y=Asin(ωx+φ)解析式的方法
若设所求解析式为y=Asin(ωx+φ),则在观察函数图象的基础上,可按以下规律来确定A,ω,φ.
(1)由函数图象上的最大值、最小值来确定|A|.
(2)由函数图象与x轴的交点确定T,由T=|ω|,确定ω.
(3)确定函数y=Asin(ωx+φ)中φ的值的两种方法:
①代入法:把图象上的一个已知点代入(此时A,ω已知,最好是代入图象与x轴的交点)求解(此时要注意交点在上升区间上还是在下降区间上).
②五点对应法:确定φ值时,往往以寻找“五点法”中的第一个零点,0作为突破口.“五点”的ωx+φ的值具体如下:
“第一点”(即图象上升时与x轴的交点)为ωx+φ=0;
“第二点”(即图象的“峰点”)为ωx+φ=2;
“第三点”(即图象下降时与x轴的交点)为ωx+φ=π;
“第四点”(即图象的“谷点”)为ωx+φ=2;
“第五点”为ωx+φ=2π.
下列函数中,图象的一部分如图所示的是( )
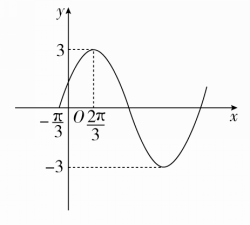
A.f(x)=3sin3
B.f(x)=3sin3
C.f(x)=3sin6
D.f(x)=3sin6
答案 C
解析 解法一(代值验证法):
把,0代入选项,可排除B,D;再将,3代入,可排除A.故C正确.
解法二(逐一定参法):
设f(x)=Asin(ωx+φ)(A>0,ω>0).
由图知,A=3,又T=43=4π,
∴ω=T=2.
由点,0,令-3×2+φ=0,得φ=6.
∴f(x)=3sin6,选C.
解法三(待定系数法):
设f(x)=Asin(ωx+φ)(A>0,ω>0),由图知,A=3.
又图象过,0,,3,根据五点法原理(这两点可理解为“五点法”中的第一点和第二点),有:
,解得ω=2,φ=6.故选C.
题型四 函数y=Asin(ωx+φ)性质的综合应用
例4 已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶函数,其图象关于点M,0对称,且在区间2上是单调函数,求φ和ω的值.
[解] ∵f(x)在R上是偶函数,
∴当x=0时,f(x)取得最大值或最小值,
即sinφ=±1,得φ=kπ+2,k∈Z.
又0≤φ≤π,∴φ=2.
由f(x)的图象关于点M,0对称,可知
sin2=0,解得ω=3k-3,k∈Z.
又f(x)在2上是单调函数,
∴T≥π,即ω≥π,∴0<ω≤2,
∴当k=1时,ω=3;当k=2时,ω=2.
综上,φ=2,ω=3或2.
金版点睛
函数y=Asin(ωx+φ)的综合运用
与正弦函数y=sinx比较可知,当ωx+φ=2kπ±2(k∈Z)时,函数y=Asin(ωx+φ)取得最大值(或最小值),因此函数y=Asin(ωx+φ)的图象的对称轴由ωx+φ=kπ+2(k∈Z)解出,其对称中心横坐标由ωx+φ=kπ(k∈Z)解出,即对称中心为,0(k∈Z).同理y=Acos(ωx+φ)的对称轴由ωx+φ=kπ(k∈Z)解出,对称中心的横坐标由ωx+φ=kπ+2(k∈Z)解出.
已知函数f(x)=2sin6+1(0<φ<π,ω>0)为偶函数,且函数f(x)的图象的两相邻对称轴间的距离为2.
(1)求f8的值;
(2)将函数f(x)的图象向右平移6个单位长度后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数g(x)的图象,求函数g(x)的单调递减区间.
解 (1)因为f(x)为偶函数,
所以φ-6=kπ+2(k∈Z),
所以φ=kπ+3(k∈Z).
又0<φ<π,所以φ=3,
所以f(x)=2sin2+1=2cosωx+1.
又函数f(x)的图象的两相邻对称轴间的距离为2,
所以T=ω=2×2,
所以ω=2,所以f(x)=2cos2x+1,
所以f8=2cos8+1=+1.
(2)将f(x)的图象向右平移6个单位长度后,得到函数f6的图象,再将所得图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到f6的图象,
所以g(x)=f6=2cos6+1
=2cos3+1.
当2kπ≤2-3≤2kπ+π(k∈Z),
即4kπ+3≤x≤4kπ+3(k∈Z)时,g(x)单调递减.
所以函数g(x)的单调递减区间是3(k∈Z).
题型五 函数y=Asin(ωx+φ)在实际生活中的应用
例5 某游乐园的摩天轮最高点距离地面108米,直径长是98米,匀速旋转一圈需要18分钟.如果某人从摩天轮的最低处登上摩天轮并开始计时,那么:

(1)当此人第四次距离地面2米时用了多少分钟?
(2)当此人距离地面不低于2米时可以看到游乐园的全貌,求摩天轮旋转一圈过程中有多少分钟可以看到游乐园的全貌?
[解] (1)如图,建立平面直角坐标系,设此人登上摩天轮t分钟时距地面y米,则α=18t=9t.
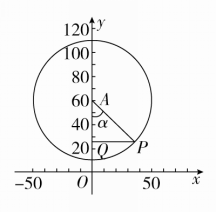
由y=108-2-2cos9t=-49cos9t+59(t≥0).
令-49cos9t+59=2,得cos9t=2,
∴9t=2kπ±3,
故t=18k±3,k∈Z,故t=3,15,21,33.
故当此人第四次距离地面2米时用了33分钟.
(2)由题意,得-49cos9t+59≥59+2,
即cos9t≤-2.
不妨在第一个周期内求即可,
所以6≤9t≤6,
解得2≤t≤2,
故2-2=3.
因此摩天轮旋转一圈过程中有3分钟可以看到游乐园的全貌.
金版点睛

如图所示,一个摩天轮半径为10 m,轮子的底部在地面上2 m处,如果此摩天轮按逆时针转动,每30 s转一圈,且当摩天轮上某人经过点P处(点P与摩天轮中心高度相同)时开始计时.
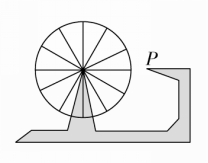
(1)求此人相对于地面的高度关于时间的关系式;
(2)在摩天轮转动的一圈内,有多长时间此人相对于地面的高度不小于17 m.
解 (1)设在t s时,摩天轮上某人在高h m处.这时此人所转过的角为30t=15t,故在t s时,此人相对于地面的高度为h=10sin15t+12(t≥0).
(2)由10sin15t+12≥17,得
sin15t≥2,则2≤t≤2.
故此人有10 s相对于地面的高度不小于17 m.
![]()
1.将函数y=sin2x的图象向左平移4个单位长度,再向上平移1个单位长度,所得到的图象对应的函数是( )
A.y=cos2x B.y=1+cos2x
C.y=1+sin4 D.y=cos2x-1
答案 B
解析 将函数y=sin2x的图象向左平移4个单位长度,得到函数y=sin4的图象,即y=sin2=cos2x的图象,再向上平移1个单位长度,所得到的图象对应的函数为y=1+cos2x.
2.已知函数f(x)=sin4(ω>0)的最小正周期为π,则该函数的图象( )
A.关于直线x=8对称 B.关于点,0对称
C.关于直线x=4对称 D.关于点,0对称
答案 A
解析 ∵ω>0,T=ω=π,∴ω=2,∴f(x)=sin4.∴其对称中心为,0,k∈Z,
故B,D不符合;其对称轴方程由2x+4=2+kπ,k∈Z得x=2+8,k∈Z.当k=0时,x=8就是它的一条对称轴.故选A.
3.为了得到y=cos4的图象,只需把y=cosx的图象上的所有点( )
A.横坐标伸长到原来的4倍,纵坐标不变
B.横坐标缩短到原来的4,纵坐标不变
C.纵坐标伸长到原来的4倍,横坐标不变
D.纵坐标缩短到原来的4,横坐标不变
答案 A
解析 由图象的周期变换可知,A正确.
4.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图,则函数f(x)的解析式为________.
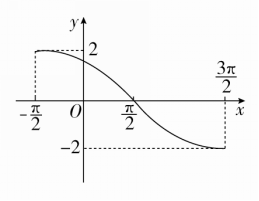
答案 f(x)=2sin4
解析 由题意,知A=2,T=22=4π,
所以ω=T=4π=2.
因为图象过点,0,
所以f2=2sin+φ=0.
因为-π<φ<π,所以φ=4或φ=-4.
又因为f2=-2,
所以φ=4,
所以f(x)=2sin4.
5.求函数f(x)=3sin3,x∈R的周期、对称中心、对称轴及单调区间.
解 T=ω=2=π,所以周期为π.
令2x+3=kπ,k∈Z,得x=2-6,k∈Z,
所以对称中心为,0,k∈Z.
令2x+3=kπ+2,k∈Z,得x=2+12,k∈Z,
所以对称轴为x=2+12,k∈Z.
令-2+2kπ≤2x+3≤2+2kπ,k∈Z,得
-12+kπ≤x≤12+kπ,k∈Z,
所以它的单调递增区间为+kπ,k∈Z;
令2+2kπ≤2x+3≤2+2kπ,k∈Z,得
12+kπ≤x≤12+kπ,k∈Z,
所以它的单调递减区间为+kπ,k∈Z.