![]() 第2课时 球的体积和表面积
第2课时 球的体积和表面积
![]()
考点 | 学习目标 | 核心素养 |
球的表面积与体积 | 记准球的表面积和体积公式,会计算球的表面积和体积 | 数学运算 |
与球有关的组合体 | 能解决与球有关的组合体的计算问题 | 数学运算、直观想象 |
![]()
![]() 问题导学
问题导学
预习教材 P117-P119 的内容,思考以下问题:
1.球的表面积公式是什么?
2.球的体积公式什么?
![]()
1.球的表面积
设球的半径为R,则球的表面积S=4πR2.
2.球的体积
设球的半径为R,则球的体积V=3πR3.
■名师点拨
对球的体积和表面积的几点认识
(1)从公式看,球的表面积和体积的大小,只与球的半径相关,给定R都有唯一确定的S和V与之对应,故表面积和体积是关于R的函数.
(2)由于球的表面不能展开成平面,所以,球的表面积公式的推导与前面所学的多面体与旋转体的表面积公式的推导方法是不一样的.
(3)球的表面积恰好是球的大圆(过球心的平面截球面所得的圆)面积的4倍.
![]()
![]() 判断(正确的打“√”,错误的打“×”)
判断(正确的打“√”,错误的打“×”)
(1)决定球的大小的因素是球的半径.( )
(2)球面被经过球心的平面截得的圆的半径等于球的半径.( )
(3)球的体积V与球的表面积S的关系为V=3S.( )
答案:(1)√ (2)√ (3)√
![]() 半径为 3 的球的体积是( )
半径为 3 的球的体积是( )
A.9π B.81π
C.27π D.36π
解析:选 D. V=3π×33=36π.
![]() 若一个球的直径为 2,则此球的表面积为( )
若一个球的直径为 2,则此球的表面积为( )
A.2π B.16π
C.8π D.4π
解析:选 D.因为球的直径为 2,所以球的半径为 1,所以球的表面积 S=4πR2=4π.
![]() 把球的表面积扩大到原来的 2 倍,那么体积扩大到原来的( )
把球的表面积扩大到原来的 2 倍,那么体积扩大到原来的( )
A.2 倍 B.2倍
C.倍 D.2倍
解析:选 B.设原球的半径为 R,表面积扩大 2 倍,则半径扩大倍,体积扩大 2倍.
![]() 如果三个球的半径之比是 1∶2∶3,那么最大球的表面积是其余两个球的表面积之和的________倍.
如果三个球的半径之比是 1∶2∶3,那么最大球的表面积是其余两个球的表面积之和的________倍.
解析:设小球半径为 1,则大球的表面积
S大=36π,S小+S中=20π,20π=5.
答案:5
![]()
![]()
球的表面积与体积
![]() (1)已知球的体积是3,则此球的表面积是( )
(1)已知球的体积是3,则此球的表面积是( )
A.12π B.16π
C.3 D.3
(2)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,若该几何体的体积是3,则它的表面积是( )
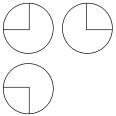
A.17π B.18π
C.20π D.28π
【解析】 (1)设球的半径为R,则由已知得
V=3πR3=3,解得R=2.
所以球的表面积S=4πR2=16π.
(2)由三视图可得此几何体为一个球切割掉8后剩下的几何体,
设球的半径为r,
故8×3πr3=3π,
所以r=2,表面积S=8×4πr2+4πr2=17π,选A.
【答案】 (1)B (2)A
![]()
球的体积与表面积的求法及注意事项
(1)要求球的体积或表面积,必须知道半径R或者通过条件能求出半径R,然后代入体积或表面积公式求解.
(2)半径和球心是球的最关键要素,把握住了这两点,计算球的表面积或体积的相关题目也就易如反掌了.
![]()
1.若一个球的表面积与其体积在数值上相等,则此球的半径为________.
解析:设此球的半径为 R,则 4πR2=3πR3,R=3.
答案:3
2.两个球的半径相差 1,表面积之差为 28π,则它们的体积和为________.
解析:设大、小两球半径分别为 R,r,
则4πR2-4πr2=28π,所以r=3.
所以体积和为 3πR3+3πr3=3.
答案:3
![]()
球的截面问题
![]()
 如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器厚度,则球的体积为( )
如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器厚度,则球的体积为( )
A.3 cm3 B.3 cm3
C.3 cm3 D.3 cm3
【解析】 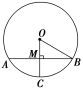 如图,作出球的一个截面,则MC=8-6=2(cm),
如图,作出球的一个截面,则MC=8-6=2(cm),
BM=2AB=2×8=4(cm).
设球的半径为R cm,则
R2=OM2+MB2
=(R-2)2+42,
所以R=5,
所以V球=3π×53=3π (cm3).
【答案】 A
![]()
球的截面问题的解题技巧
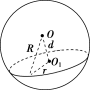 (1)有关球的截面问题,常画出过球心的截面圆,将问题转化为平面中圆的问题.
(1)有关球的截面问题,常画出过球心的截面圆,将问题转化为平面中圆的问题.
(2)解题时要注意借助球半径R,截面圆半径r,球心到截面的距离d构成的直角三角形,即R2=d2+r2.
![]() 平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
A.π B.4π
C.4π D.6π
 解析:选B.如图,设截面圆的圆心为O′,
解析:选B.如图,设截面圆的圆心为O′,
M为截面圆上任一点,
则OO′=,O′M=1.
所以OM==.
即球的半径为.
所以V=3π()3=4π.
![]()
与球有关的切、接问题
角度一 球的外切正方体问题
![]() 将棱长为 2 的正方体木块削成一个体积最大的球,则该球的体积为( )
将棱长为 2 的正方体木块削成一个体积最大的球,则该球的体积为( )
A.3 B.3
C.2 D.6
【解析】 由题意知,此球是正方体的内切球,根据其几何特征知,此球的直径与正方体的棱长是相等的,故可得球的直径为 2,故半径为 1,其体积是3×π×13=3.
【答案】 A
角度二 球的内接长方体问题
![]() 一个长方体的各个顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为 1,2,3,则此球的表面积为________.
一个长方体的各个顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为 1,2,3,则此球的表面积为________.
【解析】 长方体外接球直径长等于长方体体对角线长,即 2R==,
所以球的表面积 S=4πR2=14π.
【答案】 14π
角度三 球的内接正四面体问题
![]() 若棱长为 a 的正四面体的各个顶点都在半径为 R 的球面上,求球的表面积.
若棱长为 a 的正四面体的各个顶点都在半径为 R 的球面上,求球的表面积.
【解】 把正四面体放在正方体中,设正方体棱长为 x,则 a=x,由题意 2R=x=×2=2a,
所以 S球=4πR2=2πa2.
角度四 球的内接圆锥问题
![]() 球的一个内接圆锥满足:球心到该圆锥底面的距离是球半径的一半,则该圆锥的体积和此球体积的比值为________.
球的一个内接圆锥满足:球心到该圆锥底面的距离是球半径的一半,则该圆锥的体积和此球体积的比值为________.
【解析】 ①当圆锥顶点与底面在球心两侧时,如图所示,设球半径为 r,则球心到该圆锥底面的距离是2,于是圆锥的底面半径为 2=2,
高为2.
 该圆锥的体积为 3×π×2×2=8πr3,球体积为3πr3,所以该圆锥的体积和此球体积的比值为πr3=32.
该圆锥的体积为 3×π×2×2=8πr3,球体积为3πr3,所以该圆锥的体积和此球体积的比值为πr3=32.
②同理,当圆锥顶点与底面在球心同侧时,该圆锥的体积和此球体积的比值为32.
【答案】 32或32
角度五 球的内接直棱柱问题
![]() 设三棱柱的侧棱垂直于底面,所有棱的长都为 a,顶点都在一个球面上,则该球的表面积为( )
设三棱柱的侧棱垂直于底面,所有棱的长都为 a,顶点都在一个球面上,则该球的表面积为( )
A.πa2 B.3πa2
C.3πa2 D.5πa2
【解析】 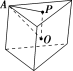 由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为 a.如图,P 为三棱柱上底面的中心,O 为球心,易知 AP=3×2a=3a,OP=2a,所以球的半径 R= OA 满足R2=a+a=12a2,故 S球=4πR2=3πa2.
由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为 a.如图,P 为三棱柱上底面的中心,O 为球心,易知 AP=3×2a=3a,OP=2a,所以球的半径 R= OA 满足R2=a+a=12a2,故 S球=4πR2=3πa2.
【答案】 B
![]()
(1)正方体的内切球
球与正方体的六个面都相切,称球为正方体的内切球,此时球的半径为 r1=2,过在一个平面上的四个切点作截面如图(1).
(2)长方体的外接球
长方体的八个顶点都在球面上,称球为长方体的外接球,根据球的定义可知,长方体的体对角线是球的直径,若长方体过同一顶点的三条棱长为 a,b,c,过球心作长方体的对角线,则球的半径为 r2=2 ,如图(2).
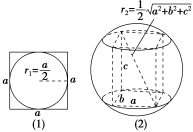
(3)正四面体的外接球
正四面体的棱长 a 与外接球半径 R 的关系为:2R=2a.
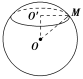
![]() 一个高为16的圆锥内接于一个体积为972π的球,在圆锥里又有一个内切球.求:
一个高为16的圆锥内接于一个体积为972π的球,在圆锥里又有一个内切球.求:
(1)圆锥的侧面积;
(2)圆锥里内切球的体积.
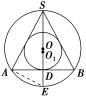 解:(1)如图所示,作出轴截面,则等腰△SAB内接于⊙O,而⊙O1内切于△SAB.
解:(1)如图所示,作出轴截面,则等腰△SAB内接于⊙O,而⊙O1内切于△SAB.
设⊙O的半径为R,
则有3πR3=972π,
所以R3=729,R=9.
所以SE=2R=18.
因为SD=16,所以ED=2.
连接AE,又因为SE是直径,
所以SA⊥AE,SA2=SD·SE=16×18=288,
所以SA=12.
因为AB⊥SD,
所以AD2=SD·DE=16×2=32,
所以AD=4.
所以S圆锥侧=π×4×12=96π.
(2)设内切球O1的半径为r,
因为△SAB的周长为2×(12+4)=32,
所以2r×32=2×8×16.所以r=4.
所以内切球O1的体积V球=3πr3=3π.
![]()
1.直径为 6 的球的表面积和体积分别是( )
A.36π,144π B.36π,36π
C.144π,36π D.144π,144π
解析:选 B.球的半径为 3,表面积 S=4π·32=36π,体积 V=3π·33=36π.
2.一个正方体的表面积与一个球的表面积相等,那么它们的体积比是( )
A.6 B.2
C.2 D.2π
解析:选 A.设正方体棱长为 a,球半径为 R,由 6a2=4πR2 得R=3,所以V2=πR3=4π3=6.
3.若两球的体积之和是 12π,经过两球球心的截面圆周长之和为 6π,则两球的半径之差为( )
A.1 B.2
C.3 D.4
解析:选 A.设两球的半径分别为 R,r(R>r),则由题意得2πR+2πr=6π,解得r=1.故 R-r=1.
4.已知棱长为 2 的正方体的体积与球 O 的体积相等,则球 O 的半径为________.
解析:设球 O 的半径为 r,则3πr3=23,
解得 r=π.
答案:π
5.已知过球面上 A,B,C 三点的截面和球心的距离为球半径的一半,且 AB=BC=CA=2,求球的表面积.
解: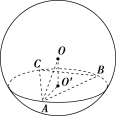 设截面圆心为O′,球心为 O,连接 O′A,OA,OO′,
设截面圆心为O′,球心为 O,连接 O′A,OA,OO′,
设球的半径为 R.
因为O′A=3×2×2=3.
在 Rt△O′OA 中,OA2=O′A2+O′O2,
所以 R2=3+4R2,
所以 R=3,
所以 S球=4πR2=9π.
![]() [A 基础达标]
[A 基础达标]
1.两个球的体积之比为8∶27,那么这两个球的表面积之比为( )
A.2∶3 B.4∶9
C.∶ D.∶
解析:选B.设两个球的半径分别为r,R,
则πr3∶πR3=r3∶R3=8∶27,
所以r∶R=2∶3,所以S1∶S2=r2∶R2=4∶9.
2.已知球的表面积为16π,则它的内接正方体的表面积S的值是( )
A.4π B.32
C.24 D.12π
解析:选B.设球的内接正方体的棱长为a,由题意知球的半径为2,则3a2=16,所以a2=3,正方体的表面积S=6a2=6×3=32.
3.用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( )
A.3 B.3
C.8π D.3
解析:选D.设截面圆的半径为r,则πr2=π,故r=1,
由勾股定理求得球的半径为=,
所以球的体积为3π()3=3,故选D.
4.把一个铁制的底面半径为r,高为h的实心圆锥熔化后铸成一个铁球,则这个铁球的半径为( )
A.2 B.4
C. 4 D.2
解析:选C.设铁球的半径为 R,因为3πr2h=3πR3,
所以R= 4.
5.已知A,B是球O的球面上两点,且球的半径为3,∠AOB=90°,C为该球面上的动点.当三棱锥OABC的体积取得最大值时,则过A,B,C三点的截面的面积为 ( )
A.6π B.12π
C.18π D.36π
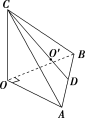 解析:选A.因为O为球心,∠AOB=90°,
解析:选A.因为O为球心,∠AOB=90°,
所以截面AOB为球大圆,
所以当动点C满足OC⊥平面OAB时,
三棱锥OABC的体积最大,
此时,OA=OB=OC=R=3,
则AB=AC=BC=3,
所以截面ABC的圆心O′为△ABC的中心,
所以圆O′的半径r=O′C=3×3=,
所以截面ABC的面积为π×()2=6π,故选A.
6.已知球面上的四点P、A、B、C,PA、PB、PC的长分别为3、4、5,且这三条线段两两垂直,则这个球的表面积为______.
解析:球面上的四点P、A、B、C,PA、PB、PC的长分别为3、4、5,且这三条线段两两垂直,是长方体的一个角,扩展为长方体,两者的外接球相同,长方体的对角线长为=5,外接球的半径为2.
外接球的表面积为4π2=50π.
答案:50π
7.若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为S1、S2,则S2=________.
解析:由题意可得圆柱的底面直径和高都与球的直径相等,设球的半径为1,则S1=6π,S2=4π.所以S2=4π=2.
答案:2
8.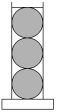 圆柱形容器内盛有高度为8 cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________cm.
圆柱形容器内盛有高度为8 cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________cm.
解析:设球的半径为x cm,由题意得πx2×8=πx2×6x-3πx3×3,解得x=4.
答案:4
9.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.
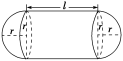
解:该组合体的表面积S=4πr2+2πrl=4π×12+2π×1×3=10π,
该组合体的体积V=3πr3+πr2l=3π×13+π×12×3=3.
10.若一个底面边长为2,侧棱长为的正六棱柱的所有顶点都在一个球面上,求该球的体积和表面积.
解: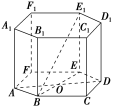 如图,在底面正六边形ABCDEF中,连接BE,AD交于O,连接BE1,则BE=2OE=2DE,所以BE=,
如图,在底面正六边形ABCDEF中,连接BE,AD交于O,连接BE1,则BE=2OE=2DE,所以BE=,
在Rt△BEE1中,
BE1==2,
所以2R=2,
则R=,
所以球的体积V球=3πR3=4π,
球的表面积S球=4πR2=12π.
[B 能力提升]
11.若等边圆柱(轴截面是正方形)、球、正方体的体积相等,则它们的表面积的大小关系是( )
A.S球<S圆柱<S正方体
B.S正方体<S球<S圆柱
C.S圆柱<S球<S正方体
D.S球<S正方体<S圆柱
解析:选A.设等边圆柱底面圆半径为r,球半径为R,正方体棱长为a,则πr2·2r=3πR3=a3,r=2,r=2π,
S圆柱=6πr2,S球=4πR2,S正方体=6a2,
S圆柱=6πr2=3·r= 3<1,
S圆柱=6πr2=π·r= π>1.故选A.
12.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积为3π,那么这个正三棱柱的体积是( )
A.96 B.16
C.24 D.48
解析:选D.由题意可知正三棱柱的高等于球的直径,从棱柱中间平行棱柱底面截得球的大圆内切于正三角形,正三角形与棱柱底的三角形全等,设三角形边长为a,球半径为r,由V球=3πr3=3π,得r=2.由S柱底=2a×r×3=4a2,得a=2r=4,所以V柱=S柱底·2r=48.
13.如图,ABCD 是正方形,︵是以 A 为圆心、AB 为半径的弧,将正方形 ABCD 以 AB 为轴旋转一周,则图中 Ⅰ、Ⅱ、Ⅲ 三部分旋转所得旋转体的体积之比为________.
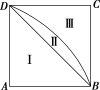
解析:Ⅰ生成圆锥,Ⅱ生成的是半球去掉圆锥Ⅰ,Ⅲ生成的是圆柱去掉扇形 ABD 生成的半球.
设正方形的边长为 a,则Ⅰ、Ⅱ、Ⅲ 三部分旋转所得旋转体的体积分别为 VⅠ、VⅡ、VⅢ,则 VⅠ=3πa3,VⅡ=3πa3÷2-3πa3=3πa3,VⅢ=πa3-3πa3÷2=3πa3.
所以三部分所得旋转体的体积之比为 1∶1∶1.
答案: 1∶1∶1
14.将一个底面圆的直径为2、高为1的圆柱截成横截面为长方形的棱柱(如图),设这个长方形截面的一条边长为x,对角线长为2,截面的面积为A.
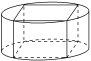
(1)求面积A以x为自变量的函数关系式;
(2)求出截得棱柱的体积的最大值.
解:(1)横截面如图长方形所示,
由题意得A=x·(0<x<2).
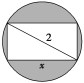
(2)V=1·x=,
由上述知0<x<2,所以当x=时,Vmax=2.
即截得棱柱的体积的最大值为2.
[C 拓展探究]
15.如图是某几何体的三视图.
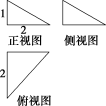
(1)求该几何体外接球的体积;
(2)求该几何体内切球的半径.
解:(1)由三视图可知,该几何体是三条侧棱两两垂直的三棱锥,如图,
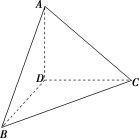
以DC,DB,DA为长、宽、高构造一个长方体,则该长方体的外接球就是该三棱锥的外接球,即外接球的半径R=2=2,
所以该几何体外接球的体积V=3πR3=2π.
(2)设内切球的球心为O,半径为r,
则VABCD=VOADB+VOADC+VODCB+VOABC.
即3×2×2×2×1
=3×2×2×2r+3×2×2×r+3×2×2×r+3×2×2×r,
得r=6=5.
所以该几何体内切球的半径为5.