![]() 8.6 空间直线、平面的垂直
8.6 空间直线、平面的垂直
8.6.1 直线与直线垂直
8.6.2 直线与平面垂直
第1课时 直线与直线垂直、直线与平面垂直的定义及判定
![]()
考点 | 学习目标 | 核心素养 |
异面直线所成的角 | 会用两条异面直线所成角的定义,找出或作出异面直线 所成的角,会在三角形中求简单的异面直线所成的角 | 直观想象、逻辑推理、 数学运算 |
直线与平面垂直的定义 | 理解并掌握直线与平面垂直的定义,明确定义中 “任意”两字的重要性 | 直观想象 |
直线与平面垂直 的判定定理 | 掌握直线与平面垂直的判定定理,并能解决有关 线面垂直的问题 | 直观想象、逻辑推理 |
![]()
![]() 问题导学
问题导学
预习教材P146-P150的内容,思考以下问题:
1.异面直线所成的角的定义是什么?
2.异面直线所成的角的范围是什么?
3.异面直线垂直的定理是什么?
4.直线与平面垂直的定义是什么?
5.直线与平面垂直的判定定理是什么?
![]()
1.异面直线所成的角
(1)定义:已知两条异面直线a,b,经过空间任一点O分别作直线a′∥a,b′∥b,把直线a′与b′所成的角叫做异面直线a与b所成的角(或夹角).
(2)垂直:如果两条异面直线所成的角是直角,就说这两条异面直线互相垂直.直线a与直线b垂直,记作a⊥b.
(3)范围:设θ为异面直线a与b所成的角,则0°<θ≤90°.
■[名师点拨]
当两条直线a,b相互平行时,规定它们所成的角为0°.所以空间两条直线所成角α的取值范围是0°≤α≤90°.注意与异面直线所成的角的范围的区别.
2.直线与平面垂直
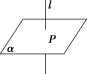
定义 | 一般地,如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直 |
记法 | l⊥α |
有关 概念 | 直线l叫做平面α的垂线,平面α叫做直线l的垂面.它们唯一的公共点P叫做垂足 |
图示 及画法 |
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直 |
■名师点拨
(1)直线与平面垂直是直线与平面相交的特殊情形.
(2)注意定义中“任意一条直线”与“所有直线”等同但不可说成“无数条直线”.
3.直线与平面垂直的判定定理
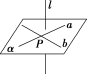
文字 语言 | 如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直 |
图形 语言 |
|
符号 语言 | l⊥a,l⊥b,a⊂α,b⊂α,a∩b=P⇒l⊥α |
■名师点拨
判定定理条件中的“两条相交直线”是关键性词语,此处强调“相交”,若两条直线平行,则直线与平面不一定垂直.
![]()
![]() 判断(正确的打“√”,错误的打“×”)
判断(正确的打“√”,错误的打“×”)
(1)异面直线a,b所成角的范围为[0°,90°].( )
(2)如果一条直线与一个平面内无数条直线都垂直,那么这条直线与这个平面垂直.( )
(3)如果一条直线与一个平面内所有直线都垂直,那么这条直线与这个平面垂直.( )
答案:(1)× (2)× (3)√
![]() 直线l与平面α内的两条直线都垂直,则直线l与平面α的位置关系是( )
直线l与平面α内的两条直线都垂直,则直线l与平面α的位置关系是( )
A.平行 .垂直
C.在平面α内 .无法确定
答案:D
![]() 已知直线a∥直线b,b⊥平面α,则( )
已知直线a∥直线b,b⊥平面α,则( )
A.a∥α .a⊂α
C.a⊥α .a是α的斜线
答案:C
![]() 在正方体ABCDA1B1C1D1中,AC与BD相交于点O,则直线OB1与A1C1所成角的度数为________.
在正方体ABCDA1B1C1D1中,AC与BD相交于点O,则直线OB1与A1C1所成角的度数为________.
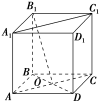
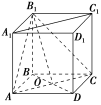 解析:连接AB1,B1C,因为AC∥A1C1,所以∠B1OC(或其补角)是异面直线OB1与A1C1所成的角.
解析:连接AB1,B1C,因为AC∥A1C1,所以∠B1OC(或其补角)是异面直线OB1与A1C1所成的角.
又因为AB1=B1C,O为AC的中点,所以B1O⊥AC,
故∠B1OC=90°,所以OB1与A1C1所成的角的大小为90°.
答案:90°
![]()
![]()
异面直线所成的角
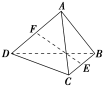
![]() 如图,在正方体ABCDEFGH中,O为侧面ADHE的中心.
如图,在正方体ABCDEFGH中,O为侧面ADHE的中心.
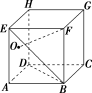
求:(1)BE与CG所成的角;
(2)FO与BD所成的角.
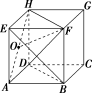 【解】 (1)如图,因为CG∥BF.
【解】 (1)如图,因为CG∥BF.
所以∠EBF(或其补角)为异面直线BE与CG所成的角,
又在△BEF中,∠EBF=45°,所以BE与CG所成的角为45°.
(2)连接FH,因为HD∥EA,EA∥FB,所以HD∥FB,又HD=FB,所以四边形HFBD为平行四边形.
所以HF∥BD,所以∠HFO(或其补角)为异面直线FO与BD所成的角.
连接HA,AF,易得FH=HA=AF,
所以△AFH为等边三角形,
又知O为AH的中点,
所以∠HFO=30°,即FO与BD所成的角为30°.
![]()
1.[变条件]在本例正方体中,若P是平面EFGH的中心,其他条件不变,求OP和CD所成的角.
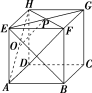 解:连接EG,HF,则P为HF的中点,连接AF,AH,OP∥AF,又CD∥AB,
解:连接EG,HF,则P为HF的中点,连接AF,AH,OP∥AF,又CD∥AB,
所以∠BAF(或其补角)为异面直线OP与CD所成的角,由于△ABF是等腰直角三角形,所以∠BAF=45°,故OP与CD所成的角为45°.
2.[变条件]在本例正方体中,若M,N分别是BF,CG的中点,且AG和BN所成的角为39.2°,求AM和BN所成的角.
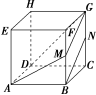 解:连接MG,因为BCGF是正方形,所以BF═∥CG,因为M,N分别是BF,CG的中点,所以BM═∥NG,所以四边形BNGM是平行四边形,所以BN∥MG,所以∠AGM(或其补角)是异面直线AG和BN所成的角,∠AMG(或其补角)是异面直线AM和BN所成的角,因为AM=MG,所以∠AGM=∠MAG=39.2°,所以∠AMG=101.6°,所以AM和BN所成的角为78.4°.
解:连接MG,因为BCGF是正方形,所以BF═∥CG,因为M,N分别是BF,CG的中点,所以BM═∥NG,所以四边形BNGM是平行四边形,所以BN∥MG,所以∠AGM(或其补角)是异面直线AG和BN所成的角,∠AMG(或其补角)是异面直线AM和BN所成的角,因为AM=MG,所以∠AGM=∠MAG=39.2°,所以∠AMG=101.6°,所以AM和BN所成的角为78.4°.

求异面直线所成的角的步骤
(1)找出(或作出)适合题设的角——用平移法,遇题设中有中点,常考虑中位线;若异面直线依附于某几何体,且对异面直线平移有困难时,可利用该几何体的特殊点,使异面直线转化为相交直线.
(2)求——转化为求一个三角形的内角,通过解三角形,求出所找的角.
(3)结论——设由(2)所求得的角的大小为θ.若0°<θ≤90°,则θ为所求;若90°<θ<180°,则180°-θ为所求.
 [提醒] 求异面直线所成的角,通常把异面直线平移到同一个三角形中去,通过解三角形求得,但要注意异面直线所成的角θ的范围是0°<θ≤90°.
[提醒] 求异面直线所成的角,通常把异面直线平移到同一个三角形中去,通过解三角形求得,但要注意异面直线所成的角θ的范围是0°<θ≤90°.
![]() 如图所示,在三棱锥ABCD中,AB=CD,AB⊥CD,E,F分别为BC,AD的中点,求EF与AB所成的角.
如图所示,在三棱锥ABCD中,AB=CD,AB⊥CD,E,F分别为BC,AD的中点,求EF与AB所成的角.
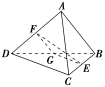 解:如图所示,取BD的中点G,连接EG,FG.
解:如图所示,取BD的中点G,连接EG,FG.
因为E,F分别为BC,AD的中点,AB=CD,
所以EG∥CD,GF∥AB,
且EG=2CD,GF=2AB.
所以∠GFE(或其补角)就是异面直线EF与AB所成的角,EG=GF.
因为AB⊥CD,所以EG⊥GF.
所以∠EGF=90°.
所以△EFG为等腰直角三角形.
所以∠GFE=45°,
即EF与AB所成的角为45°.
![]()
直线与平面垂直的定义
![]() (1)直线l⊥平面α,直线m⊂α,则l与m不可能( )
(1)直线l⊥平面α,直线m⊂α,则l与m不可能( )
A.平行 .相交
C.异面 .垂直
(2)设l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
A.若l⊥m,m⊂α,则l⊥α B.若l⊥α,l∥m,则m⊥α
C.若l∥α,m⊂α,则l∥m D.若l∥α,m∥α,则l∥m
【解析】 (1)因为直线l⊥平面α,所以l与α相交.
又因为m⊂α,所以l与m相交或异面.
由直线与平面垂直的定义,可知l⊥m.
故l与m不可能平行.
(2)对于A,直线l⊥m,m并不代表平面α内任意一条直线,所以不能判定线面垂直;对于B,因为l⊥α,则l垂直于α内任意一条直线,又l∥m,由异面直线所成角的定义知,m与平面α内任意一条直线所成的角都是90°,即m⊥α,故B正确;对于C,也有可能是l,m异面;对于D,l,m还可能相交或异面.
【答案】 (1)A (2)B
![]()
对线面垂直定义的理解
(1)直线和平面垂直的定义是描述性定义,对直线的任意性要注意理解.实际上,“任何一条”与“所有”表达相同的含义.当直线与平面垂直时,该直线就垂直于这个平面内的任何直线.由此可知,如果一条直线与一个平面内的一条直线不垂直,那么这条直线就一定不与这个平面垂直.
(2)由定义可得线面垂直⇒线线垂直,即若a⊥α,b⊂α,则a⊥b.
![]() 下列命题中,正确的序号是________.
下列命题中,正确的序号是________.
①若直线l与平面α内的一条直线垂直,则l⊥α;
②若直线l不垂直于平面α,则α内没有与l垂直的直线;
③若直线l不垂直于平面α,则α内也可以有无数条直线与l垂直;
④若平面α内有一条直线与直线l不垂直,则直线l与平面α不垂直.
解析:当l与α内的一条直线垂直时,不能保证l与平面α垂直,所以①不正确;当l与α不垂直时,l可能与α内的无数条平行直线垂直,所以②不正确,③正确.根据线面垂直的定义,若l⊥α,则l与α内的所有直线都垂直,所以④正确.
答案:③④
![]()
直线与平面垂直的判定
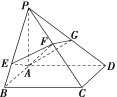
![]() 如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于点E,AF⊥PC于点F.
如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于点E,AF⊥PC于点F.
(1)求证:PC⊥平面AEF;
(2)设平面AEF交PD于点G,求证:AG⊥PD.
【证明】 (1)因为PA⊥平面ABCD,BC⊂平面ABCD,所以PA⊥BC.
又AB⊥BC,PA∩AB=A,
所以BC⊥平面PAB,AE⊂平面PAB,
所以AE⊥BC.又AE⊥PB,PB∩BC=B,
所以AE⊥平面PBC,PC⊂平面PBC,
所以AE⊥PC.
又因为PC⊥AF,AE∩AF=A,
所以PC⊥平面AEF.
(2)由(1)知PC⊥平面AEF,又AG⊂平面AEF,
所以PC⊥AG,
同理CD⊥平面PAD,AG⊂平面PAD,
所以CD⊥AG,又PC∩CD=C,
所以AG⊥平面PCD,PD⊂平面PCD,
所以AG⊥PD.
![]()
1.[变条件]在本例中,底面ABCD是菱形,H是线段AC上任意一点,其他条件不变,求证:BD⊥FH.
证明:因为四边形ABCD是菱形,所以BD⊥AC,
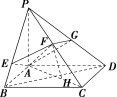 又PA⊥平面ABCD,
又PA⊥平面ABCD,
BD⊂平面ABCD,
所以BD⊥PA,
因为PA∩AC=A,
所以BD⊥平面PAC,又FH⊂平面PAC,
所以BD⊥FH.
2.[变条件]若本例中PA=AD,G是PD的中点,其他条件不变,求证:PC⊥平面AFG.
证明:因为PA⊥平面ABCD,DC⊂平面ABCD,所以DC⊥PA,
又因为ABCD是矩形,所以DC⊥AD,又PA∩AD=A,
所以DC⊥平面PAD,又AG⊂平面PAD,
所以AG⊥DC,
因为PA=AD,G是PD的中点,
所以AG⊥PD,又DC∩PD=D,
所以AG⊥平面PCD,所以PC⊥AG,
又因为PC⊥AF,AG∩AF=A,
所以PC⊥平面AFG.
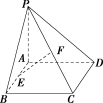 3.[变条件]本例中的条件“AE⊥PB于点E,AF⊥PC于点F”,改为“E,F分别是AB,PC的中点,PA=AD”,其他条件不变,求证:EF⊥平面PCD.
3.[变条件]本例中的条件“AE⊥PB于点E,AF⊥PC于点F”,改为“E,F分别是AB,PC的中点,PA=AD”,其他条件不变,求证:EF⊥平面PCD.
证明:取PD的中点G,连接AG,FG.
因为G,F分别是PD,PC的中点,
所以GF═∥2CD,又AE═∥2CD,所以GF═∥AE,
所以四边形AEFG是平行四边形,所以AG∥EF.
因为PA=AD,G是PD的中点,
所以AG⊥PD,所以EF⊥PD,
易知CD⊥平面PAD,AG⊂平面PAD,
所以CD⊥AG,所以EF⊥CD.
因为PD∩CD=D,所以EF⊥平面PCD.
![]()
(1)线线垂直和线面垂直的相互转化

(2)证明线面垂直的方法
①线面垂直的定义.
②线面垂直的判定定理.
③如果两条平行直线的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面.
④如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面.
[提醒] 要证明两条直线垂直(无论它们是异面还是共面),通常是证明其中的一条直线垂直于另一条直线所在的一个平面.
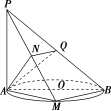
![]() 如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,M为圆周上任意一点,AN⊥PM,N为垂足.
如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,M为圆周上任意一点,AN⊥PM,N为垂足.
(1)求证:AN⊥平面PBM;
(2)若AQ⊥PB,垂足为Q,求证:NQ⊥PB.
证明:(1)因为AB为⊙O的直径,
所以AM⊥BM.又PA⊥平面ABM,所以PA⊥BM.
又因为PA∩AM=A,所以BM⊥平面PAM.
又AN⊂平面PAM,所以BM⊥AN.
又AN⊥PM,且BM∩PM=M,
所以AN⊥平面PBM.
(2)由(1)知AN⊥平面PBM,
PB⊂平面PBM,所以AN⊥PB.
又因为AQ⊥PB,AN∩AQ=A,
所以PB⊥平面ANQ.
又NQ⊂平面ANQ,所以NQ⊥PB.
![]()
1.若直线a⊥平面α,b∥α,则a与b的关系是( )
A.a⊥b,且a与b相交
B.a⊥b,且a与b不相交
C.a⊥b
D.a与b不一定垂直
解析:选C.过直线b作一个平面β,使得β∩α=c,则b∥c.因为直线a⊥平面α,c⊂α,所以a⊥c.因为b∥c,所以a⊥b.当b与a相交时为相交垂直,当b与a不相交时为异面垂直.
2.在正方体ABCDA1B1C1D1中,与AD1垂直的平面是( )
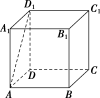
A.平面DD1C1C .平面A1DB1
C.平面A1B1C1D1 .平面A1DB
解析:选B.因为AD1⊥A1D,AD1⊥A1B1,且A1D∩A1B1=A1,所以AD1⊥平面A1DB1.
3.空间四边形的四边相等,那么它的对角线( )
A.相交且垂直 .不相交也不垂直
C.相交不垂直 .不相交但垂直
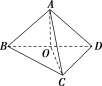 解析:选D.如图,空间四边形ABCD,假设AC与BD相交,则它们共面α,从而四点A,B,C,D都在α内,这与ABCD为空间四边形矛盾,所以AC与BD不相交;取BD的中点O,连接OA与OC,因为AB=AD=DC=BC,所以AO⊥BD,OC⊥BD,从而可知BD⊥平面AOC,故AC⊥BD.
解析:选D.如图,空间四边形ABCD,假设AC与BD相交,则它们共面α,从而四点A,B,C,D都在α内,这与ABCD为空间四边形矛盾,所以AC与BD不相交;取BD的中点O,连接OA与OC,因为AB=AD=DC=BC,所以AO⊥BD,OC⊥BD,从而可知BD⊥平面AOC,故AC⊥BD.
4.已知a,b是一对异面直线,而且a平行于△ABC的边AB所在的直线,b平行于边AC所在的直线,若∠BAC=120°,则直线a,b所成的角为________.
解析:由a∥AB,b∥AC,∠BAC=120°,知异面直线a,b所成的角为∠BAC的补角,所以直线a,b所成的角为60°.
答案:60°
![]()
[A 基础达标]
1.已知m和n是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中,一定能推出m⊥β的是( )
A.α∥β,且m⊂α .m∥n,且n⊥β
C.m⊥n,且n⊂β .m⊥n,且n∥β
解析:选B.A中,由α∥β,且m⊂α,知m∥β;B中,由n⊥β,知n垂直于平面β内的任意直线,再由m∥n,知m也垂直于β内的任意直线,所以m⊥β,B符合题意;C,D中,m⊂β或m∥β或m与β相交,不符合题意.故选B.
2.已知直线a∥b,平面α∥β,a⊥α,则b与β的位置关系是( )
A.b⊥β .b∥β
C.b⊂β .b⊂β或b∥β
解析:选A.因为a⊥α,a∥b,所以b⊥α.又α∥β,所以b⊥β.
3.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q分别为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不垂直的是( )
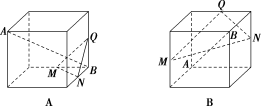
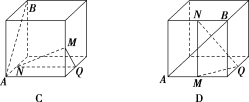
解析:选D.对于A,易证AB⊥MN,AB⊥NQ,即可得直线AB⊥平面MNQ;对于B,易证AB⊥MN,AB⊥NQ,即可得直线AB⊥平面MNQ;对于C,易证AB⊥NQ,AB⊥MQ,即可得直线AB⊥平面MNQ;对于D,由图可得MN与直线AB相交且不垂直,故直线AB与平面MNQ不垂直.故选D.
4.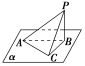 如图,P为△ABC所在平面α外一点,PB⊥α,PC⊥AC,则△ABC的形状为( )
如图,P为△ABC所在平面α外一点,PB⊥α,PC⊥AC,则△ABC的形状为( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
解析:选B.由PB⊥α,AC⊂α得PB⊥AC,
又AC⊥PC,PC∩PB=P,
所以AC⊥平面PBC,AC⊥BC.故选B.
5.在正方体ABCDA1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是 ( )
A.线段B1C
B.线段BC1
C.BB1中点与CC1中点连成的线段
D.BC中点与B1C1中点连成的线段
解析:选A.如图,由于BD1⊥平面AB1C,故点P一定位于线段B1C上.
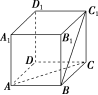
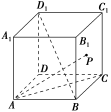
6.如图,在正方形ABCDA1B1C1D1中,AC与BC1所成角的大小是______.
解析:连接AD1,则AD1∥BC1.
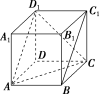 所以∠CAD1(或其补角)就是AC与BC1所成的角,连接CD1,在正方体ABCDA1B1C1D1中,AC=AD1=CD1,
所以∠CAD1(或其补角)就是AC与BC1所成的角,连接CD1,在正方体ABCDA1B1C1D1中,AC=AD1=CD1,
所以∠CAD1=60°,
即AC与BC1所成的角为60°.
答案:60°
7.如图,∠BCA=90°,PC⊥平面ABC,则在△ABC,△PAC的边所在的直线中:
(1)与PC垂直的直线有__________________;
(2)与AP垂直的直线有__________________.
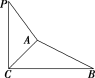
解析:(1)因为PC⊥平面ABC,AB,AC,BC⊂平面ABC.所以PC⊥AB,PC⊥AC,PC⊥BC.
(2)∠BCA=90°即BC⊥AC,又BC⊥PC,
AC∩PC=C,所以BC⊥平面PAC,因为AP⊂平面PAC,所以BC⊥AP.
答案:(1)AB,AC,BC (2)BC
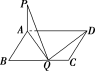 8.如图所示,在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD,且PA=1,若BC边上存在点Q,使得PQ⊥QD,则a的最小值为________.
8.如图所示,在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD,且PA=1,若BC边上存在点Q,使得PQ⊥QD,则a的最小值为________.
解析:因为PA⊥平面ABCD,所以PA⊥QD.
若BC边上存在一点Q,使得QD⊥PQ,PA∩PQ=P,
则有QD⊥平面PAQ,从而QD⊥AQ.
在矩形ABCD中,当AD=a<2时,直线BC与以AD为直径的圆相离,故不存在点Q,使PQ⊥DQ.
所以当a≥2时,才存在点Q,使得PQ⊥QD.所以a的最小值为2.
答案:2
9. 如图,在直三棱柱ABCA1B1C1中,∠BAC=90°,AB=AC,D是BC的中点,点E在棱BB1上运动.证明:AD⊥C1E.
如图,在直三棱柱ABCA1B1C1中,∠BAC=90°,AB=AC,D是BC的中点,点E在棱BB1上运动.证明:AD⊥C1E.
证明:因为AB=AC,D是BC的中点,
所以AD⊥BC.①
又在直三棱柱ABCA1B1C1中,BB1⊥平面ABC,
而AD⊂平面ABC,所以AD⊥BB1.②
由①②得AD⊥平面BB1C1C.
由点E在棱BB1上运动,得C1E⊂平面BB1C1C,
所以AD⊥C1E.
10.如图所示,等腰直角三角形ABC中,∠BAC=90°,BC=,DA⊥AC,DA⊥AB,若DA=1,且E为DA的中点,求异面直线BE与CD所成角的余弦值.
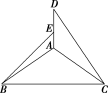
解:取AC的中点F,连接EF,BF,
在△ACD中,E,F分别是AD,AC的中点,
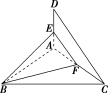
所以EF∥CD,
所以∠BEF(或其补角)即为所求的异面直线BE与CD所成的角.
在Rt△ABC中,BC=,AB=AC,
所以AB=AC=1,
在Rt△EAB中,AB=1,AE=2AD=2,
所以BE=2.
在Rt△AEF中,AF=2AC=2,AE=2,
所以EF=2.
在Rt△ABF中,AB=1,AF=2,所以BF=2.
在等腰三角形EBF中,cos∠FEB=BE=2=10,
所以异面直线BE与CD所成角的余弦值为10.
[B 能力提升]
11.已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a,b所成的角都是30°的直线有且仅有( )
A.1条 B.2条
C.3条 D.4条
解析:选B.过空间一点P,作a′∥a,b′∥b.由a′、b′两交线确定平面α,a′与b′的夹角为50°,则过角的平分线与直线a′、b′所在的平面α垂直的平面上,角平分线的两侧各有一条直线与a′、b′成30°的角,即与a、b成30°的角且过点P的直线有两条.
在a′、b′相交另一个130°的角部分内不存在与a′、b′成30°角的直线.故应选B.
12.(2018·高考全国卷Ⅱ)在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=,则异面直线AD1与DB1所成角的余弦值为( )
A.5 B.6
C.5 D.2
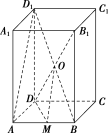 解析:选C.如图,连接BD1,交DB1于O,取AB的中点M,连接DM,OM,易知O为BD1的中点,所以AD1∥OM,则∠MOD为异面直线AD1与DB1所成角.因为在长方体ABCDA1B1C1D1中,AB=BC=1,AA1=,AD1=11=2,DM=2=2,DB1=11=,所以OM=2AD1=1,OD=2DB1=2,于是在△DMO中,由余弦定理,得
解析:选C.如图,连接BD1,交DB1于O,取AB的中点M,连接DM,OM,易知O为BD1的中点,所以AD1∥OM,则∠MOD为异面直线AD1与DB1所成角.因为在长方体ABCDA1B1C1D1中,AB=BC=1,AA1=,AD1=11=2,DM=2=2,DB1=11=,所以OM=2AD1=1,OD=2DB1=2,于是在△DMO中,由余弦定理,得
cos∠MOD=5=5,即异面直线AD1与DB1所成角的余弦值为5,故选C.
13.如图,在矩形ABCD中,AB=8,BC=4,E为DC边的中点,沿AE将△ADE折起,在折起过程中,下列结论正确的有( )

①ED⊥平面ACD;②CD⊥平面BED;③BD⊥平面ACD;④AD⊥平面BED.
A.1个 B.2个
C.3个 D.4个
解析:选A.因为在矩形ABCD中,AB=8,BC=4,E为DC边的中点,
所以在折起过程中,D点在平面ABCE上的投影如图.
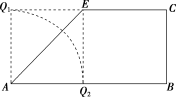
因为DE与AC所成角不能为直角,
所以DE不会垂直于平面ACD,故①错误;
只有D点投影位于Q2位置时,即平面AED与平面AEB重合时,
才有BE⊥CD,此时CD不垂直于平面AECB,
故CD与平面BED不垂直,故②错误;
BD与AC所成角不能为直角,
所以BD不能垂直于平面ACD,故③错误;
因为AD⊥ED,并且在折起过程中,有AD⊥BD,
所以存在一个位置使AD⊥BE,
所以在折起过程中有AD⊥平面BED,故④正确.故选A.
14.如图,在多面体ABCDEF中,已知四边形ABCD是边长为2的正方形,△BCF为正三角形,G,H分别为BC,EF的中点,EF=4且EF∥AB,EF⊥FB.
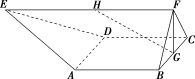
(1)求证:GH∥平面EAD;
(2)求证:FG⊥平面ABCD.
证明:(1)如图,取AD的中点M,连接EM,GM.
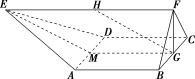
因为EF∥AB,M,G分别为AD,BC的中点,所以MG∥EF.
因为H为EF的中点,EF=4,AB=2,
所以EH=AB=MG,所以四边形EMGH为平行四边形,所以GH∥EM,
又因为GH⊄平面EAD,EM⊂平面EAD,
所以GH∥平面EAD.
(2)因为EF⊥FB,EF∥AB,所以AB⊥FB.
在正方形ABCD中,AB⊥BC,所以AB⊥平面FBC.
又FG⊂平面FBC,所以AB⊥FG.
在正三角形FBC中,FG⊥BC,所以FG⊥平面ABCD.
[C 拓展探究]
15.如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.
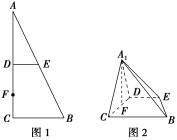
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.
解:(1)证明:因为D,E分别为AC,AB的中点,
所以DE∥BC.
又因为DE⊄平面A1CB,BC⊂平面A1CB,
所以DE∥平面A1CB.
(2)证明:由已知得AC⊥BC且DE∥BC,
所以DE⊥AC.
因为DE⊥A1D,DE⊥CD,所以DE⊥平面A1DC.
而A1F⊂平面A1DC,所以DE⊥A1F.
又因为A1F⊥CD,CD∩DE=D,所以A1F⊥平面BCDE.
所以A1F⊥BE.
 (3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:
(3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:
如图,分别取A1C,A1B的中点P,Q,
则PQ∥BC.
又因为DE∥BC,所以DE∥PQ.
所以平面DEQ即为平面DEQP.
由(2)知,DE⊥平面A1DC,所以DE⊥A1C.
又因为P是等腰△DA1C底边A1C的中点,
所以A1C⊥DP.又DP∩DE=D,
所以A1C⊥平面DEQP.即A1C⊥平面DEQ.
故线段A1B上存在点Q,使得A1C⊥平面DEQ.