![]() 10.1.3 古典概型
10.1.3 古典概型
![]()
考点 | 学习目标 | 核心素养 |
基本事件 | 了解基本事件的特点 | 数学抽象 |
古典概型的定义 | 理解古典概型的定义 | 数学抽象 |
古典概型的概率公式 | 会应用古典概型的概率公式解决实际问题 | 数学运算、数学建模 |
![]()
![]() 问题导学
问题导学
预习教材P233-P238的内容,思考以下问题:
1.古典概型的定义是什么?
2.古典概型有哪些特征?
3.古典概型的计算公式是什么?
![]()
1.古典概型
具有以下特征的试验叫做古典概型试验,其数学模型称为古典概率模型,简称古典概型.
(1)有限性:样本空间的样本点只有有限个;
(2)等可能性:每个样本点发生的可能性相等.
■名师点拨
古典概型的判断
一个试验是否为古典概型,在于这个试验是否具有古典概型的两个特点:有限性和等可能性.并不是所有的试验都是古典概型.
下列三类试验都不是古典概型:
①样本点个数有限,但非等可能.
②样本点个数无限,但等可能.
③样本点个数无限,也不等可能.
2.古典概型的概率公式
一般地,设试验E是古典概型,样本空间Ω包含n个样本点,事件A包含其中的k个样本点,则定义事件A的概率
P(A)=n=n(Ω).
其中,n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
![]()
![]() 同时投掷两枚大小完全相同的骰子,用(x,y)表示结果,记A为“所得点数之和小于5”,则事件A包含的基本事件数是( )
同时投掷两枚大小完全相同的骰子,用(x,y)表示结果,记A为“所得点数之和小于5”,则事件A包含的基本事件数是( )
A.3 B.4 C.5 D.6
解析:选D.事件A包含的基本事件有6个:(1,1),(1,2),(1,3),(2,1),(2,2),(3,1).故选D.
![]() 若书架上放有数学、物理、化学书分别是5本、3本、2本,则随机抽出一本是物理书的概率为( )
若书架上放有数学、物理、化学书分别是5本、3本、2本,则随机抽出一本是物理书的概率为( )
A.5 B.10
C.5 D.2
解析:选B.基本事件总数为10,“抽出一本是物理书”包含3个基本事件,所以其概率为10,故选B.
![]() (2019·河北省石家庄市期末考试)将一枚骰子连续抛掷两次,则向上点数之差的绝对值不大于3的概率是( )
(2019·河北省石家庄市期末考试)将一枚骰子连续抛掷两次,则向上点数之差的绝对值不大于3的概率是( )
A.3 B.6
C.36 D.4
解析:选B.由题意,连续抛掷两次骰子共有6×6=36种情况;绝对值大于3的有(1,5),(1,6),(2,6),(5,1),(6,1),(6,2)共6种,所以绝对值不大于3有:36-6=30种,故所求概率P=36=6.故选B.
![]() 下列概率模型:
下列概率模型:
①在平面直角坐标系内,从横坐标和纵坐标都是整数的所有点中任取一点;
②某射手射击一次,可能命中0环,1环,2环,…,10环;
③某小组有男生5人,女生3人,从中任选1人做演讲;
④一只使用中的灯泡的寿命长短;
⑤中秋节前夕,某市工商部门调查辖区内某品牌的月饼质量,给该品牌月饼评“优”或“差”.
其中属于古典概型的是________.
解析:①不属于,原因是所有横坐标和纵坐标都是整数的点有无限多个,不满足有限性;②不属于,原因是命中0环,1环,…,10环的概率不一定相同,不满足等可能性;③属于,显然满足有限性和等可能性;④不属于,原因是灯泡的寿命是任何一个非负实数,有无限多种可能,不满足有限性;⑤不属于,原因是该品牌月饼被评为“优”或“差”的概率不一定相同,不满足等可能性.
答案:③
![]()
![]()
样本点的列举
![]() 一只口袋内装有5个大小相同的球,白球3个,黑球2个,从中一次摸出2个球.
一只口袋内装有5个大小相同的球,白球3个,黑球2个,从中一次摸出2个球.
(1)共有多少个样本点?
(2)“2个都是白球”包含几个样本点?
【解】 (1)法一:采用列举法.
分别记白球为1,2,3号,黑球为4,5号,则样本点如下:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10个(其中(1,2)表示摸到1号,2号球).
法二:采用列表法.
设5个球的编号分别为a,b,c,d,e,其中a,b,c为白球,d,e为黑球.列表如下:
a | b | c | d | e | |
a | (a,b) | (a,c) | (a,d) | (a,e) | |
b | (b,a) | (b,c) | (b,d) | (b,e) | |
c | (c,a) | (c,b) | (c,d) | (c,e) | |
d | (d,a) | (d,b) | (d,c) | (d,e) | |
e | (e,a) | (e,b) | (e,c) | (e,d) |
由于每次取2个球,每次所取2个球不相同,而摸到(b,a)与(a,b)是相同的事件,故共有10个样本点.
(2)法一中“2个都是白球”包括(1,2),(1,3),(2,3),共3个样本点,法二中“2个都是白球”包括(a,b),(b,c),(a,c),共3个样本点.
![]()
样本点的三种列举方法
(1)直接列举法:把试验的全部结果一一列举出来.此方法适合于较为简单的试验问题.
(2)列表法:将样本点用表格的方式表示出来,通过表格可以弄清样本点的总数,以及要求的事件所包含的样本点数.列表法适用于较简单的试验的题目,样本点较多的试验不适合用列表法.
(3)树状图法:树状图法是使用树状的图形把样本点列举出来的一种方法,树状图法便于分析样本点间的结构关系,对于较复杂的问题,可以作为一种分析问题的主要手段,树状图法适用于较复杂的试验的题目.
![]() 袋中有2个标号分别为1,2的白球和2个标号分别为3,4的黑球.这4个球除颜色、标号外完全相同,4个人按顺序依次从中摸出1个球,求样本点的个数.
袋中有2个标号分别为1,2的白球和2个标号分别为3,4的黑球.这4个球除颜色、标号外完全相同,4个人按顺序依次从中摸出1个球,求样本点的个数.
解:4个人按顺序依次从袋中摸出1个球的所有可能结果用树状图表示如图所示:
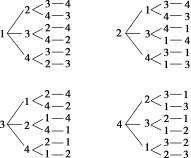
共24个样本点.
![]()
古典概型的概率计算
![]() (1)有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为( )
(1)有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为( )
A.5 B.5
C.5 D.5
(2)(2018·高考江苏卷)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为________.
【解析】 (1)从5支彩笔中任取2支不同颜色的彩笔,有10种不同取法:(红,黄),(红,蓝),(红,绿),(红,紫),(黄,蓝),(黄,绿),(黄,紫),(蓝,绿),(蓝,紫),(绿,紫).而取出的2支彩笔中含有红色彩笔的取法有(红,黄),(红,蓝),(红,绿),(红,紫),共4种,故所求概率P=10=5.
(2)记2名男生分别为A,B,3名女生分别为a,b,c,则从中任选2名学生有AB,Aa,Ab,Ac,Ba,Bb,Bc,ab,ac,bc,共10种情况,其中恰好选中2名女生有ab,ac,bc,共3种情况,故所求概率为10.
【答案】 (1)C (2)10
![]()
求古典概型概率的步骤
(1)判断是否为古典概型.
(2)算出样本点的总数n.
(3)算出事件A中包含的样本点个数m.
(4)算出事件A的概率,即P(A)=n.
在运用公式计算时,关键在于求出m,n.在求n时,应注意这n种结果必须是等可能的,在这一点上比较容易出错.
![]()
1.如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( )
A.10 B.5
C.10 D.20
解析:选C.从1,2,3,4,5中任取3个不同的数,共有如下10个不同的结果:(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5),其中勾股数只有(3,4,5),所以概率为10.故选C.
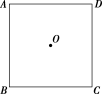
2.从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离不小于该正方形边长的概率为( )
A.5 B.5
C.5 D.5
解析:选C.如图可知从5个点中选取2个点的全部情况有(O,A),(O,B),(O,C),(O,D),(A,B),(A,C),(A,D),(B,C),(B,D),(C,D),共10种.
选取的2个点的距离不小于该正方形边长的情况有(A,B),(A,C),(A,D),(B,C),(B,D),(C,D),共6种.故所求概率为10=5.
![]()
数学建模——古典概型的实际应用
![]() 已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层随机抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层随机抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
【解】 (1)由已知,甲,乙,丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层随机抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人.
(2)(i)从抽出的7名同学中随机抽取2名同学的所有可能结果为
(A,B),(A,C),(A,D),(A,E),(A,F),(A,G),(B,C),(B,D),(B,E),(B,F),(B,G),(C,D),(C,E),(C,F),(C,G),(D,E),(D,F),(D,G),(E,F),(E,G),(F,G),共21种.
(ii)由(1)设抽出的7名同学中,来自甲年级的是A,B,C,来自乙年级的是D,E,来自丙年级的是F,G,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为(A,B),(A,C),(B,C),(D,E),(F,G),共5种.所以事件M发生的概率P(M)=21.
![]()
如何建立概率模型(古典概型)
(1)在建立概率模型(古典概型)时,把什么看作一个样本点(即一个试验结果)是人为规定的.我们只要求每次试验有且只有一个样本点出现.对于同一个随机试验,可以根据需要(建立概率模型的主观原因)建立满足我们要求的概率模型.
(2)注意验证是否满足古典概型的两个特性,即①样本点的有限性;②每个样本点发生的可能性相等.
(3)求解时将其转化为互斥事件或对立事件的概率问题.
![]() (2019·高考天津卷)2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
(2019·高考天津卷)2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
员工 项目 | A | B | C | D | E | F |
子女教育 | ○ | ○ | × | ○ | × | ○ |
继续教育 | × | × | ○ | × | ○ | ○ |
大病医疗 | × | × | × | ○ | × | × |
住房贷款利息 | ○ | ○ | × | × | ○ | ○ |
住房租金 | × | × | ○ | × | × | × |
赡养老人 | ○ | ○ | × | × | × | ○ |
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.
解:(1)由已知,老、中、青员工人数之比为6∶9∶10,由于采用分层抽样的方法从中抽取25位员工,因此应从老、中、青员工中分别抽取6人,9人,10人.
(2)①从已知的6人中随机抽取2人的所有可能结果为(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15种.
②由表格知,符合题意的所有可能结果为(A,B),(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,E),(C,F),(D,F),(E,F),共11种.
所以事件M发生的概率P(M)=15.
![]()
1.下列是古典概型的是( )
①从6名同学中,选出4人参加数学竞赛,每人被选中的可能性的大小.
②同时掷两颗骰子,点数和为7的概率.
③近三天中有一天降雨的概率.
④10个人站成一排,其中甲、乙相邻的概率.
A.①②③④ B.①②④
C.②③④ D.①③④
解析:选B.①②④为古典概型,因为都适合古典概型的两个特征:有限性和等可能性,而③不适合等可能性,故不为古典概型.
2.甲、乙两人有三个不同的学习小组A,B,C可以参加,若每人必须参加并且仅能参加一个学习小组(两人参加各个小组的可能性相同),则两人参加同一个学习小组的概率为 ( )
A.3 B.4 C.5 D.6
解析:选A.甲乙两人参加学习小组,若以(A,B)表示甲参加学习小组A,乙参加学习小组B,则一共有如下情形:(A,A),(A,B),(A,C),(B,A),(B,B),(B,C),(C,A),(C,B),(C,C),共有9种情形,其中两人参加同一个学习小组共有3种情形,根据古典概型概率公式,得P=3.
3.从甲、乙、丙、丁、戊五个人中选取三人参加演讲比赛,则甲、乙都当选的概率为( )
A.5 B.5 C.10 D.5
解析:选C.从五个人中选取三人有10种不同结果:(甲,乙,丙),(甲,乙,丁),(甲,乙,戊),(甲,丙,丁),(甲,丙,戊),(甲,丁,戊),(乙,丙,丁),(乙,丙,戊),(乙,丁,戊),(丙,丁,戊),而甲、乙都当选的结果有3种,故所求的概率为10.
4.在1,2,3,4四个数中,可重复地选取两个数,其中一个数是另一个数的2倍的概率是________.
解析:可重复地选取两个数共有16种可能,其中一个数是另一个数的2倍的有1,2;2,1;2,4;4,2共4种,故所求的概率为16=4.
答案:4
5.一只口袋装有形状大小都相同的6只小球,其中2只白球,2只红球,2只黄球,从中随机摸出2只球,试求:
(1)2只球都是红球的概率;
(2)2只球同色的概率;
(3)“恰有一只是白球”是“2只球都是白球”的概率的几倍?
解:记两只白球分别为a1,a2;两只红球分别为b1,b2;两只黄球分别为c1,c2.
从中随机取2只球的所有结果为(a1,a2),(a1,b1),(a1,b2),(a1,c1),(a1,c2),(a2,b1),(a2,b2),(a2,c1),(a2,c2),(b1,b2),(b1,c1),(b1,c2),(b2,c1),(b2,c2),(c1,c2)共15种结果.
(1)2只球都是红球为(b1,b2)共1种,
故2只球都是红球的概率P=15.
(2)2只球同色的有:(a1,a2),(b1,b2),(c1,c2),共3种,
故2只球同色的概率P=15=5.
(3)恰有一只是白球的有:(a1,b1),(a1,b2),(a1,c1),(a1,c2),(a2,b1),(a2,b2),(a2,c1),(a2,c2),共8种,其概率P=15;
2只球都是白球的有:(a1,a2),1种,故概率P=15,
所以“恰有一只是白球”是“2只球都是白球”的概率的8倍.
![]()
[A 基础达标]
1.(2019·高考全国卷Ⅱ)生物实验室有5只兔子,其中只有3只测量过某项指标.若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为( )
A.3 B.5
C.5 D.5
解析:选B.设3只测量过某项指标的兔子为A,B,C,另2只兔子为a,b,从这5只兔子中随机取出3只,则样本点共有10种,分别为(A,B,C),(A,B,a),(A,B,b),(A,C,a),(A,C,b),(A,a,b),(B,C,a),(B,C,b),(B,a,b),(C,a,b),其中“恰有2只测量过该指标”的取法有6种,分别为(A,B,a),(A,B,b),(A,C,a),(A,C,b),(B,C,a),(B,C,b),因此所求的概率为10=5,选B.
2.(2019·高考全国卷Ⅲ)两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是( )
A.6 B.4
C.3 D.2
解析:选D.将两位男同学分别记为A1,A2,两位女同学分别记为B1,B2,则四位同学排成一列,情况有A1A2B1B2,A1A2B2B1,A2A1B1B2,A2A1B2B1,A1B1A2B2,A1B2A2B1,A2B1A1B2,A2B2A1B1,B1A1A2B2,B1A2A1B2,B2A1A2B1,B2A2A1B1,A1B1B2A2,A1B2B1A2,A2B1B2A1,A2B2B1A1,B1B2A1A2,B1B2A2A1,B2B1A1A2,B2B1A2A1,B1A1B2A2,B1A2B2A1,B2A1B1A2,B2A2B1A1,共有24种,其中2名女同学相邻的有12种,所以所求概率P=2,故选D.
3.(2019·福建省三明市质量检测)同时投掷两个骰子,向上的点数分别记为a,b,则方程2x2+ax+b=0有两个不等实根的概率为( )
A.5 B.4
C.3 D.2
解析:选B.因为方程2x2+ax+b=0有两个不等实根,所以Δ=a2-8b>0,
又同时投掷两个骰子,向上的点数分别记为a,b,则共包含36个样本点,
满足a2-8b>0的有(6,1),(6,2),(6,3),(6,4),(5,1),(5,2),(5,3),(4,1),(3,1)共9个样本点,所以方程2x2+ax+b=0有两个不等实根的概率为36=4.故选B.
4.某部三册的小说,任意排放在书架的同一层上,则各册从左到右或从右到左恰好为第1,2,3册的概率为( )
A.6 B.3
C.2 D.3
解析:选B.所有样本点为(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1).其中从左到右或从右到左恰好为第1,2,3册包含2个样本点,所以P=6=3.故选B.
5.(2019·河北省沧州市期末考试)定义:abcde=10 000a+1 000b+100c+10d+e,当五位数abcde满足a<b<c,且c>d>e时,称这个五位数为“凸数”.由1,2,3,4,5组成的没有重复数字的五位数共120个,从中任意抽取一个,则其恰好为“凸数”的概率为( )
A.6 B.10
C.12 D.20
解析:选D.由题意,由1,2,3,4,5组成的没有重复数字的五位数恰好为“凸数”的有:12543,13542,14532,23541,24531,34521,共6个样本点,所以恰好为“凸数”的概率为P=120=20.故选D.
6.(2019·湖北省四地七校联考)掷两颗均匀的骰子,则点数之和为6的概率等于________.
解析:掷两颗均匀的骰子,共有36个样本点,点数之和为6的样本点有(1,5),(2,4),(3,3),(4,2),(5,1)这五种,因此所求概率为36.
答案:36
7.(2019·广西钦州市期末考试)在某学校图书馆的书架上随意放着编号为1,2,3,4,5的五本书,若某同学从中任意选出2本书,则选出的2本书编号相连的概率为________.
解析:从五本书中任意选出2本书的所有可能情况为(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)、(3,4)、(3,5)、(4,5)共10种,
满足2本书编号相连的所有可能情况为(1,2)、(2,3)、(3,4)、(4,5)共4种,
故选出的2本书编号相连的概率为10=5.
答案:5
8.某城市有8个商场A,B,C,D,E,F,G,H和市中心O排成如图所示的格局,其中每个小方格为正方形,某人从网格中随机地选择一条最短路径,欲从商场A前往商场H,则他经过市中心O的概率为________.
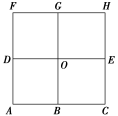
解析:此人从商场A前往商场H的所有最短路径有A→B→C→E→H,A→B→O→E→H,A→B→O→G→H,A→D→O→E→H,A→D→O→G→H,A→D→F→G→H,共6条,其中经过市中心O的有4条,所以所求概率为3.
答案:3
9.(2019·广西钦州市期末考试)将一颗质地均匀的骰子先后抛掷2次,观察向上的点数,并分别记为x,y.
(1)若记“x+y=5”为事件A,求事件A发生的概率;
(2)若记“x2+y2≤10”为事件B,求事件B发生的概率.
解:将一颗质地均匀的骰子抛掷1次,它的点数有1、2、3、4、5、6这6种结果,
抛掷第2次,它的点数有1、2、3、4、5、6这6种结果,
因为骰子共抛掷2次,所以共有6×6=36种结果.
(1)事件A发生的样本点有(1,4)、(2,3)、(4,1)、(3,2)共4种结果,
所以事件A发生的概率为P(A)=36=9.
(2)事件B发生的样本点有(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)共6种结果,所以事件B发生的概率为P(B) =36=6.
10.某市举行职工技能比赛活动,甲厂派出2男1女共3名职工,乙厂派出2男2女共4名职工.
(1)若从甲厂和乙厂报名的职工中各任选1名进行比赛,求选出的2名职工性别相同的概率;
(2)若从甲厂和乙厂报名的这7名职工中任选2名进行比赛,求选出的这2名职工来自同一工厂的概率.
解:记甲厂派出的2名男职工为A1,A2,1名女职工为a;乙厂派出的2名男职工为B1,B2,2名女职工为b1,b2.
(1)从甲厂和乙厂报名的职工中各任选1名,不同的结果有(A1,B1),(A1,B2),(A1,b1),(A1,b2),(A2,B1),(A2,B2),(A2,b1),(A2,b2),(a,B1),(a,B2),(a,b1),(a,b2),共12种.其中选出的2名职工性别相同的选法有(A1,B1),(A1,B2),(A2,B1),(A2,B2),(a,b1),(a,b2),共6种.
故选出的2名职工性别相同的概率P=12=2.
(2)若从甲厂和乙厂报名的这7名职工中任选2名,不同的结果有(A1,A2),(A1,a),(A1,B1),(A1,B2),(A1,b1),(A1,b2),(A2,a),(A2,B1),(A2,B2),(A2,b1),(A2,b2),(a,B1),(a,B2),(a,b1),(a,b2),(B1,B2),(B1,b1),(B1,b2),(B2,b1),(B2,b2),(b1,b2),共21种.
其中选出的2名职工来自同一工厂的选法有(A1,A2),(A1,a),(A2,a),(B1,B2),(B1,b1),(B1,b2),(B2,b1),(B2,b2),(b1,b2),共9种.
故选出的2名职工来自同一工厂的概率为P=21=7.
[B 能力提升]
11.古代“五行”学说认为:“物质分金、木、水、火、土五种属性,金克木、木克土、土克水、水克火、火克金.”从五种不同属性的物质中随机抽取两种,则抽取的两种物质不相克的概率为( )
A.10 B.5
C.2 D.5
解析:选C.从五种不同属性的物质中随机抽取两种,有(金,木)、(金,水)、(金,火)、(金,土)、(木,水)、(木,火)、(木,土)、(水,火)、(水,土)、(火,土)共10种等可能发生的结果,其中金克木,木克土,土克水,水克火,火克金,即相克的有5种,则不相克的也是5种,所以抽取的两种物质不相克的概率为2.
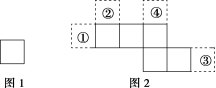
12.(2019·江西省上饶市期末统考)图1和图2中所有的正方形都全等,图1中的正方形放在图2中的①②③④某一位置,所组成的图形能围成正方体的概率是( )
A.4 B.2
C.4 D.1
解析:选A.由题意,可得样本点的总数为n=4,
又由题图1中的正方形放在题图2中的①处时,所组成的图形不能围成正方体;
题图1中的正方形放在题图2中的②③④处的某一位置时,所组成的图形能围成正方体,
所以将题图1中的正方形放在题图2中的①②③④的某一位置,所组成的图形能围成正方体的概率为P=4.故选A.
13.设a是从集合{1,2,3,4}中随机取出的一个数,b是从集合{1,2,3}中随机取出的一个数,构成一个样本点(a,b).记“这些样本点中,满足logba≥1”为事件E,则E发生的概率是________.
解析:事件E发生包含的样本点是分别从两个集合中取一个数字,共有12种结果,满足条件的样本点是满足logba≥1,可以列举出所有的样本点,当b=2时,a=2,3,4,当b=3时,a=3,4,共有3+2=5个,所以根据古典概型的概率公式得到概率是12.
答案:12
14.某校从高二甲、乙两班各选出3名学生参加书画比赛,其中从高二甲班选出了1名女同学、2名男同学,从高二乙班选出了1名男同学、2名女同学.
(1)若从这6名同学中抽出2名进行活动发言,写出所有可能的结果,并求高二甲班女同学、高二乙班男同学至少有一人被选中的概率;
(2)若从高二甲班和乙班各选1名同学现场作画,写出所有可能的结果,并求选出的2名同学性别相同的概率.
解:(1)设选出的3名高二甲班同学为A,B,C,其中A为女同学,B,C为男同学,选出的3名高二乙班同学为D,E,F,其中D为男同学,E,F为女同学.从这6名同学中抽出2人的所有可能结果有(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15种.
其中高二甲班女同学、高二乙班男同学至少有一人被选中的可能结果有(A,B),(A,C),(A,D),(A,E),(A,F),(B,D),(C,D),(D,E),(D,F),共9种,
故高二甲班女同学、高二乙班男同学至少有一人被选中的概率P=15=5.
(2)高二甲班和乙班各选1名的所有可能结果为(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),共9种,
选出的2名同学性别相同的有(A,E),(A,F),(B,D),(C,D),共4种,所以选出的2名同学性别相同的概率为9.
[C 拓展探究]
15.在某亲子游戏结束时有一项抽奖活动,抽奖规则是:盒子里面共有4个小球,小球上分别写有0,1,2,3的数字,小球除数字外其他完全相同,每对亲子中,家长先从盒子中取出一个小球,记下数字后将小球放回,孩子再从盒子中取出一个小球,记下小球上数字将小球放回.①若取出的两个小球上数字之积大于4,则奖励飞机玩具一个;②若取出的两个小球上数字之积在区间[1,4]上,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于1,则奖励饮料一瓶.
(1)求每对亲子获得飞机玩具的概率;
(2)试比较每对亲子获得汽车玩具与获得饮料的概率,哪个更大?请说明理由.
解:样本空间Ω={(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3),(2,0),(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3)}共16个样本点.
(1)记“获得飞机玩具”为事件A,事件A包含的样本点有(2,3),(3,2),(3,3)共3个.
故每对亲子获得飞机玩具的概率为P(A)=16.
(2)记“获得汽车玩具”为事件B,记“获得饮料”为事件C.
事件B包含的样本点有
(1,1),(1,2),(1,3),(2,1),(2,2),(3,1)共6个.
所以P(B)=16=8,
事件C包含的样本点有(0,0),(0,1),(0,2),(0,3),(1,0),(2,0),(3,0)共7个,
所以P(C)= 6.
所以P(B)<P(C),
即每对亲子获得饮料的概率大于获得汽车玩具的概率.