![]() 10.2 事件的相互独立性
10.2 事件的相互独立性
![]()
考点 | 学习目标 | 核心素养 |
相互独立事件的概念 | 理解相互独立事件的概念及意义 | 数学抽象 |
相互独立事件同时发生的概念 | 能记住相互独立事件概率的乘法公式; 能综合运用互斥事件的概率加法公式 及独立事件的乘法公式解题 | 数学运算、数学建模 |
![]()
![]() 问题导学
问题导学
预习教材P247~P249的内容,思考以下问题:
1.事件的相互独立性的定义是什么?
2.相互独立事件有哪些性质?
3.相互独立事件与互斥事件有什么区别?
![]()
1.相互独立的概念
设A,B为两个事件,若P(AB)=P(A)P(B),则称事件A与事件B相互独立.
2.相互独立的性质
若事件A与B相互独立,那么A与-,-与B,-与-也都相互独立.
■名师点拨 (1)必然事件Ω,不可能事件∅都与任意事件相互独立.
(2)事件A,B相互独立的充要条件是P(AB)=P(A)·P(B).
![]()
![]() 判断(正确的打“√”,错误的打“×”)
判断(正确的打“√”,错误的打“×”)
(1)不可能事件与任何一个事件相互独立.( )
(2)必然事件与任何一个事件相互独立.( )
(3)“P(AB)=P(A)·P(B)”是“事件A,B相互独立”的充要条件.( )
答案:(1)√ (2)√ (3)√
![]() 下列事件A,B是相互独立事件的是( )
下列事件A,B是相互独立事件的是( )
A.一枚硬币掷两次,A表示“第一次为正面”,B表示“第二次为反面”
B.袋中有2个白球,2个黑球,不放回地摸球两次,每次摸一球,A表示“第一次摸到白球”,B表示“第二次摸到白球”
C.掷一枚骰子,A表示“出现点数为奇数”,B表示“出现点数为偶数”
D.A表示“一个灯泡能用1 000小时”,B表示“一个灯泡能用2 000小时”
答案:A
![]() 甲、乙两水文站同时作水文预报,如果甲站、乙站各自预报的准确率为0.8和0.7.那么,在一次预报中,甲、乙两站预报都准确的概率为________.
甲、乙两水文站同时作水文预报,如果甲站、乙站各自预报的准确率为0.8和0.7.那么,在一次预报中,甲、乙两站预报都准确的概率为________.
答案:0.56
![]() 一件产品要经过两道独立的工序,第一道工序的次品率为a,第二道工序的次品率为b,则该产品的正品率为________.
一件产品要经过两道独立的工序,第一道工序的次品率为a,第二道工序的次品率为b,则该产品的正品率为________.
答案:(1-a)(1-b)
![]()
![]()
相互独立事件的判断
![]() 一个家庭中有若干个小孩,假定生男孩和生女孩是等可能的,令A={一个家庭中既有男孩又有女孩},B={一个家庭中最多有一个女孩}.对下述两种情形,讨论A与B的独立性:
一个家庭中有若干个小孩,假定生男孩和生女孩是等可能的,令A={一个家庭中既有男孩又有女孩},B={一个家庭中最多有一个女孩}.对下述两种情形,讨论A与B的独立性:
(1)家庭中有两个小孩;
(2)家庭中有三个小孩.
【解】 (1)有两个小孩的家庭,男孩、女孩的可能情形为Ω={(男,男),(男,女),(女,男),(女,女)},
它有4个基本事件,由等可能性知概率都为4.
这时A={(男,女),(女,男)},
B={(男,男),(男,女),(女,男)},
AB={(男,女),(女,男)},
于是P(A)=2,P(B)=4,P(AB)=2.
由此可知P(AB)≠P(A)P(B),
所以事件A,B不相互独立.
(2)有三个小孩的家庭,小孩为男孩、女孩的所有可能情形为Ω={(男,男,男),(男,男,女),(男,女,男),(男,女,女),(女,男,男),(女,男,女),(女,女,男),(女,女,女)}.
由等可能性知这8个基本事件的概率均为8,这时A中含有6个基本事件,B中含有4个基本事件,AB中含有3个基本事件.
于是P(A)=8=4,P(B)=8=2,P(AB)=8,
显然有P(AB)=8=P(A)P(B)成立.
从而事件A与B是相互独立的.
![]()
判断两个事件是否相互独立的两种方法
(1)根据问题的实质,直观上看一事件的发生是否影响另一事件发生的概率来判断,若没有影响,则两个事件就是相互独立事件;
(2)定义法:通过式子P(AB)=P(A)P(B)来判断两个事件是否独立,若上式成立,则事件A,B相互独立,这是定量判断.
![]()
1.分别抛掷两枚质地均匀的硬币,设事件A是“第一枚为正面”,事件B是“第二枚为正面”,事件C是“两枚结果相同”,则下列事件具有相互独立性的有________.(填序号)
①A,B;②A,C;③B,C.
解析:根据事件相互独立的定义判断,只要P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C)成立即可.利用古典概型概率公式计算可得P(A)=0.5,P(B)=0.5,P(C)=0.5,P(AB)=0.25,P(AC)=0.25,P(BC)=0.25.可以验证P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C).所以根据事件相互独立的定义,事件A与B相互独立,事件B与C相互独立,事件A与C相互独立.
答案:①②③
2.从一副扑克牌(52张)中任抽一张,记事件A为“抽得K”,记事件B为“抽得红牌”,记事件C为“抽得J”.判断下列每对事件是否相互独立?为什么?
(1)A与B;
(2)C与A.
解:(1)P(A)=52=13,P(B)=52=2.事件AB即为“既抽得K又抽得红牌”,亦即“抽得红桃K或方块K”,故P(AB)=52=26,从而有P(A)P(B)=P(AB),因此事件A与B相互独立.
(2)事件A与事件C是互斥的,因此事件A与C不是相互独立事件.
![]()
相互独立事件同时发生的概率
![]() 王敏某天乘火车从重庆到上海去办事,若当天从重庆到上海的三列火车正点到达的概率分别为0.8,0.7,0.9,假设这三列火车之间是否正点到达互不影响.求:
王敏某天乘火车从重庆到上海去办事,若当天从重庆到上海的三列火车正点到达的概率分别为0.8,0.7,0.9,假设这三列火车之间是否正点到达互不影响.求:
(1)这三列火车恰好有两列正点到达的概率;
(2)这三列火车至少有一列正点到达的概率.
【解】 用A,B,C分别表示这三列火车正点到达的事件.
则P(A)=0.8,P(B)=0.7,P(C)=0.9,
所以P(-)=0.2,P(-)=0.3,P(-)=0.1.
(1)由题意得A,B,C之间互相独立,所以恰好有两列正点到达的概率为
P1=P(-BC)+P(A-C)+P(AB-)=
P(-)P(B)P(C)+P(A)P(-)P(C)+P(A)P(B)P(-)
=0.2×0.7×0.9+0.8×0.3×0.9+0.8×0.7×0.1=0.398.
(2)三列火车至少有一列正点到达的概率为
P2=1-P(---)=1-P(-)P(-)P(-)
=1-0.2×0.3×0.1=0.994.
![]()
1.[变问法]在本例条件下,求恰有一列火车正点到达的概率.
解:恰有一列火车正点到达的概率为
P3=P(A--)+P(-B-)+P(--C)=P(A)P(-)P(-)+P(-)P(B)P(-)+P(-)P(-)P(C)=0.8×0.3×0.1+0.2×0.7×0.1+0.2×0.3×0.9=0.092.
2.[变条件]若一列火车正点到达记10分,用ξ表示三列火车的总得分,求P(ξ≤20).
解:事件“ξ≤20”表示“至多两列火车正点到达”,其对立事件为“三列火车都正点到达”,所以P(ξ≤20)=1-P(ABC)=1-P(A)P(B)P(C)
=1-0.8×0.7×0.9=0.496.
![]()
与相互独立事件有关的概率问题的求解策略
明确事件中的“至少有一个发生”“至多有一个发生”“恰好有一个发生”“都发生”“都不发生”“不都发生”等词语的意义.
一般地,已知两个事件A,B,它们的概率分别为P(A),P(B),那么:
(1)A,B中至少有一个发生为事件A+B.
(2)A,B都发生为事件AB.
(3)A,B都不发生为事件--.
(4)A,B恰有一个发生为事件A-+- B.
(5)A,B中至多有一个发生为事件A-+-B+- -.
它们之间的概率关系如表所示:
A,B互斥 | A,B相互独立 | |
P(A+B) | P(A)+P(B) | 1-P(-)P(-) |
P(AB) | 0 | P(A)P(B) |
P(A B) | 1-[P(A)+P(B)] | P(-)P(-) |
![]() 甲、乙2个人独立地破译一个密码,他们能译出密码的概率分别为3和4,求:
甲、乙2个人独立地破译一个密码,他们能译出密码的概率分别为3和4,求:
(1)2个人都译出密码的概率;
(2)2个人都译不出密码的概率;
(3)至多有1个人译出密码的概率;
(4)恰有1个人译出密码的概率;
(5)至少有1个人译出密码的概率.
解:记“甲独立地译出密码”为事件A,“乙独立地译出密码”为事件B,A与B为相互独立事件,且P(A)=3,P(B)=4.
(1)“2个人都译出密码”的概率为
P(AB)=P(A)·P(B)=3×4=12.
(2)“2个人都译不出密码”的概率为
P(--)=P(-)·P(-)=[1-P(A)]×[1-P(B)]=(1-3)×(1-4)=2.
(3)“至多有1个人译出密码”的对立事件为“2个人都译出密码”,
所以至多1个人译出密码的概率为
1-P(AB)=1-P(A)P(B)=1-3×4=12.
(4)“恰有1个人译出密码”可以分为两类,即甲译出乙未译出以及甲未译出乙译出,且两个事件为互斥事件,
所以恰有1个人译出密码的概率为
P(A-+-B)=P(A-)+P(-B)
=P(A)P(-)+P(-)P(B)
=3×(1-4)+(1-3)×4=12.
(5)“至少有1个人译出密码”的对立事件为“2个人都未译出密码”,
所以至少有1个人译出密码的概率为
1-P(--)=1-P(-)P(-)=1-3×4=2.
![]()
相互独立事件的综合应用
![]() 本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租用时间不超过两小时免费,超过两小时的部分每小时收费2元(不足一小时的部分按一小时计算).有甲、乙两人独立来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为4,2,超过两小时但不超过三小时还车的概率分别为2,4,两人租车时间都不会超过四小时.
本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租用时间不超过两小时免费,超过两小时的部分每小时收费2元(不足一小时的部分按一小时计算).有甲、乙两人独立来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为4,2,超过两小时但不超过三小时还车的概率分别为2,4,两人租车时间都不会超过四小时.
(1)求甲、乙两人所付租车费用相同的概率;
(2)设ξ为甲、乙两人所付的租车费用之和,求P(ξ=4)和P(ξ=6)的值.
【解】 (1)由题意可得甲、乙两人超过三小时但不超过四小时还车的概率分别为4,4.
记甲、乙两人所付的租车费用相同为事件A,则P(A)=4×2+2×4+4×4=16.所以甲、乙两人所付租车费用相同的概率为16.
(2)P(ξ=4)=4×4+2×4+2×4=16,
P(ξ=6)=4×4+2×4=16.
![]()
概率问题中的数学思想
(1)正难则反.灵活应用对立事件的概率关系(P(A)+P(-)=1)简化问题,是求解概率问题最常用的方法.
(2)化繁为简.将复杂事件的概率转化为简单事件的概率,即寻找所求事件与已知事件之间的关系.“所求事件”分几类(考虑加法公式转化为互斥事件)还是分几步组成(考虑乘法公式转化为相互独立事件).
(3)方程思想.利用有关的概率公式和问题中的数量关系,建立方程(组),通过解方程(组)使问题获解.
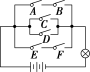
![]() 一个电路如图所示,A,B,C,D,E,F为6个开关,其闭合的概率都是2,且是相互独立的,则灯亮的概率是( )
一个电路如图所示,A,B,C,D,E,F为6个开关,其闭合的概率都是2,且是相互独立的,则灯亮的概率是( )
A.64 B.64
C.8 D.16
解析:选B.设A与B中至少有一个不闭合的事件为T,E与F中至少有一个不闭合的事件为R,则P(T)=P(R)=1-2×2=4,所以灯亮的概率
P=1-P(T)P(R)P(C)P(D)=64.
![]() ,
,
1.如图,在两个圆盘中,指针落在圆盘每个数所在区域的机会均等,那么两个指针同时落在奇数所在区域的概率是( )
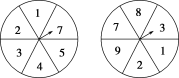
A.9 B.9
C.3 D.3
解析:选A.左边圆盘指针落在奇数区域的概率为6=3,右边圆盘指针落在奇数区域的概率也为3,所以两个指针同时落在奇数区域的概率为3×3=9.
2.已知A,B是相互独立事件,且P(A)=2,P(B)=3,则P(A-)=________;P(- -)=________.
解析:因为P(A)=2,P(B)=3.
所以P(-)=2,P(-)=3.
所以P(A -)=P(A)P(-)=2×3=6,P(- -)=P(-)P(-)=2×3=6.
答案:6 6
3.某人忘记了电话号码的最后一个数字,因而他随意地拨号,假设拨过了的号码不再重复,试求下列事件的概率:
(1)第3次拨号才接通电话;
(2)拨号不超过3次而接通电话.
解:设Ai={第i次拨号接通电话},i=1,2,3.
(1)第3次才接通电话可表示为-- A3,
于是所求概率为P(--A3)=10×9×8=10.
(2)拨号不超过3次而接通电话可表示为A1+- A2+--A3,
于是所求概率为P(A1+-A2+--A3)
=P(A1)+P(-A2)+P(--A3)
=10+10×9+10×9×8=10.
![]() [A 基础达标]
[A 基础达标]
1.坛子中放有3个白球,2个黑球,从中进行不放回地取球两次,每次取一球,用A1表示第一次取得白球,A2表示第二次取得白球,则A1和A2是( )
A.互斥事件 B.相互独立事件
C.对立事件 D.不相互独立的事件
解析:选D.因为P(A1)=5,若A1发生了,P(A2)=4=2;若A1不发生,P(A2)=4,所以A1发生的结果对A2发生的结果有影响,所以A1与A2不是相互独立事件.
2.某人提出一个问题,甲先答,答对的概率为0.4,如果甲答错,由乙答,答对的概率为0.5,则问题由乙答对的概率为( )
A.0.2 B.0.8 C.0.4 D.0.3
解析:选D.由相互独立事件同时发生的概率可知,问题由乙答对的概率为P=0.6×0.5=0.3,故选D.
3.某种开关在电路中闭合的概率为p,现将4只这种开关并联在某电路中(如图所示),若该电路为通路的概率为81,则p=( )
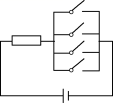
A.2 B.3 C.3 D.4
解析:选B.因为该电路为通路的概率为81,所以该电路为不通路的概率为1-81,只有当并联的4只开关同时不闭合时该电路不通路,所以1-81=(1-p)4,解得p=3或p=3(舍去).故选B.
4.(2019·重庆检测)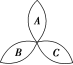 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一片荷叶跳到另一片荷叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A荷叶上,则跳三次之后停在A荷叶上的概率是( )
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一片荷叶跳到另一片荷叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A荷叶上,则跳三次之后停在A荷叶上的概率是( )
A.3 B.9 C.9 D.27
解析:选A.由已知得逆时针跳一次的概率为3,顺时针跳一次的概率为3,则逆时针跳三次停在A上的概率为P1=3×3×3=27,顺时针跳三次停在A上的概率为P2=3×3×3=27.所以跳三次之后停在A上的概率为P=P1+P2=27+27=3.
5.有一道数学难题,学生A解出的概率为2,学生B解出的概率为3,学生C解出的概率为4.若A,B,C三人独立去解答此题,则恰有一人解出的概率为( )
A.1 B.4 C.24 D.24
解析:选C.一道数学难题,恰有一人解出,包括:
①A解出,B,C解不出,概率为2×3×4=4;
②B解出,A,C解不出,概率为2×3×4=8;
③C解出,A,B解不出,概率为2×3×4=12.
所以恰有1人解出的概率为4+8+12=24.
6.有甲、乙两批种子,发芽率分别为0.8和0.9,在两批种子中各取一粒,则恰有一粒种子能发芽的概率是________.
解析:所求概率P=0.8×0.1+0.2×0.9=0.26.
答案:0.26
7.在如图所示的电路图中,开关a,b,c闭合与断开的概率都是2,且是相互独立的,则灯亮的概率是________.
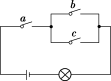
解析:设“开关a,b,c闭合”分别为事件A,B,C,则灯亮这一事件为ABC∪AB-∪A- C,且A,B,C相互独立,
ABC,AB-,A- C相互独立,
ABC,AB-,A- C互斥,所以
P=P(ABC)+P(AB-)+P(A-C)
=P(A)P(B)P(C)+P(A)P(B)P(-)+P(A)P(-)P(C)
=2×2×2+2×2×2+2×2×2=8.
答案:8
8.某大街在甲、乙、丙三处设有红绿灯,汽车在这三处因遇绿灯而通行的概率分别为3,2,3,则汽车在这三处因遇红灯或黄灯而停车一次的概率为________.
解析:分别设汽车在甲、乙、丙三处通行的事件为A,B,C,
则P(A)=3,P(B)=2,P(C)=3,
停车一次为事件(-BC)∪(A-C)∪(AB-),
故其概率P=3×2×3+3×2×3+3×2×3=18.
答案:18
9.某学生语、数、英三科考试成绩在一次考试中排名全班第一的概率为语文为0.9,数学为0.8,英语为0.85,求在一次考试中:
(1)三科成绩均未获得第一名的概率是多少?
(2)恰有一科成绩未获得第一名的概率是多少?
解:分别记该学生语、数、英考试成绩排名全班第一的事件为A,B,C,则A,B,C两两互相独立,
且P(A)=0.9,P(B)=0.8,P(C)=0.85.
(1)“三科成绩均未获得第一名”可以用- - -表示,
P(- - -)=P(-)P(-)P(-)
=[1-P(A)][1-P(B)][1-P(C)]
=(1-0.9)(1-0.8)(1-0.85)
=0.003,
即三科成绩均未获得第一名的概率是0.003.
(2)“恰有一科成绩未获得第一名”可以用
(-BC)∪(A-C)∪(AB-)表示.
由于事件-BC,A-C和AB-两两互斥,
根据概率加法公式和相互独立事件的意义,所求的概率为P(-BC)+P(A-C)+P(AB-)
=P(-)P(B)P(C)+P(A)P(-)P(C)+P(A)P(B)P(-)
=[1-P(A)]P(B)P(C)+P(A)[1-P(B)]P(C)+P(A)P(B)[1-P(C)]
=(1-0.9)×0.8×0.85+0.9×(1-0.8)×0.85+0.9×0.8×(1-0.85)=0.329,
即恰有一科成绩未获得第一名的概率是0.329.
10.某田径队有三名短跑运动员,根据平时训练情况统计甲、乙、丙三人100 m跑(互不影响)的成绩在13 s内(称为合格)的概率分别为5,4,3,若对这三名短跑运动员的100 m跑的成绩进行一次检测,则
(1)三人都合格的概率;
(2)三人都不合格的概率;
(3)出现几人合格的概率最大.
解:记“甲、乙、丙三人100 m跑成绩合格”分别为事件A,B,C,显然事件A,B,C相互独立,
则P(A)=5,P(B)=4,P(C)=3.
设恰有k人合格的概率为Pk(k=0,1,2,3),
(1)三人都合格的概率为
P3=P(ABC)=P(A)·P(B)·P(C)=5×4×3=10.
(2)三人都不合格的概率为
P0=P(---)=P(-)·P(-)·P(-)=5×4×3=10.
(3)恰有两人合格的概率为
P2=P(AB-)+P(A -C)+P(-BC)
=5×4×3+5×4×3+5×4×3=60.
恰有一人合格的概率为
P1=1-P0-P2-P3=1-10-60-10=60=12.
综合(1)(2)(3)可知P1最大.
所以出现恰有1人合格的概率最大.
[B 能力提升]
11.端午节放假,甲回老家过节的概率为3,乙、丙回老家过节的概率分别为4,5.假定三人的行动相互之间没有影响,那么这段时间内至少有1人回老家过节的概率为( )
A.60 B.5 C.2 D.60
解析:选B.“甲、乙、丙回老家过节”分别记为事件A,B,C,则P(A)=3,P(B)=4,P(C)=5,所以P(-)=3,P(-)=4,P(-)=5.由题知A,B,C为相互独立事件,所以三人都不回老家过节的概率P(---)=P(-)P(-)P(-)=3×4×5=5,所以至少有1人回老家过节的概率P=1-5=5.
12.如图,已知电路中4个开关闭合的概率都是2,且是互相独立的,则灯亮的概率为( )
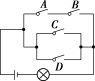
A.16 B.4 C.16 D.4
解析:选C.记“A,B,C,D四个开关闭合”分别为事件A,B,C,D,可用对立事件求解,图中含开关的三条线路同时断开的概率为P(-)P(-)[1-P(AB)]=2×2×2=16.所以灯亮的概率为1-16=16.
13.事件A,B,C相互独立,如果P(AB)=6,P(-C)=8,P(AB-)=8,则P(B)=________,P(-B)=________.
解析:由题意可得,
解得P(A)=3,P(B)=2,P(C)=4,
所以P(-B)=P(-)·P(B)=3×2=3.
答案:2 3
14.在社会主义新农村建设中,某市决定在一个乡镇投资农产品加工、绿色蔬菜种植和水果种植三个项目,据预测,三个项目成功的概率分别为5、6、3,且三个项目是否成功互相独立.
(1)求恰有两个项目成功的概率;
(2)求至少有一个项目成功的概率.
解:(1)只有农产品加工和绿色蔬菜种植两个项目成功的概率为
5×6×(1-3)=9,
只有农产品加工和水果种植两个项目成功的概率为
5×(1-6)×3=45,
只有绿色蔬菜种植和水果种植两个项目成功的概率为
(1-5)×6×3=9,
所以恰有两个项目成功的概率为9+45+9=45.
(2)三个项目全部失败的概率为
(1-5)×(1-6)×(1-3)=90,
所以至少有一个项目成功的概率为1-90=90.
[C 拓展探索]
15.甲、乙两人各进行一次射击,如果两人击中目标的概率都是0.8,计算:
(1)两人都击中目标的概率;
(2)其中恰有一人击中目标的概率;
(3)至少有一人击中目标的概率.
解:记“甲射击一次,击中目标”为事件A,“乙射击一次,击中目标”为事件B.“两人都击中目标”是事件AB;“恰有1人击中目标”是A-∪-B;“至少有1人击中目标”是AB∪A-∪-B.
(1)“两人各射击一次,都击中目标”就是事件AB,又由于事件A与B相互独立.
所以P(AB)=P(A)·P(B)=0.8×0.8=0.64.
(2)“两人各射击一次,恰好有一人击中目标”包括两种情况:一种是甲击中乙未击中(即A-),另一种是甲未击中乙击中(即-B).根据题意,这两种情况在各射击一次时不可能同时发生,即事件A-与-B是互斥的,所以所求概率为P=P(A-)+P(-B)=P(A)·P(-)×P(-)·P(B)=0.8×(1-0.8)+(1-0.8)×0.8=0.16+0.16=0.32.
(3)“两人各射击一次,至少有一人击中目标”的概率为P=P(AB)+[P(A-)+P(-B)]=0.64+0.32=0.96.