一周强化

一、一周知识概述

　　本章首先在平面直角坐标系中，介绍直线的倾斜角、斜率等概念；然后建立直线的方程：点斜式、斜截式、两点式、截距式等；通过直线的方程，研究直线间的位置关系：平行和垂直．本章自始至终贯穿数形结合的思想．在图形的研究过程中，注意代数方法的使用；在代数方法的使用过程中，加强与图形的联系．

二、重难点知识归纳

1．倾斜角

　　(1)定义

　　当直线l与x轴相交时，取x轴作为基准，x轴正向与直线l向上方向之间所成的角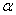叫做直线l的倾斜角．

　　当直线与x轴平行或重合时，规定它的倾斜角为．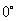

　　(2)倾斜角相同的直线是一组平行线．确定一条直线的几何要素是：直线上的一个定点以及它的倾斜角，两者缺一不可．

2．斜率

　　(1)定义

　　倾斜角不是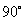的直线，它的倾斜角的正切值叫做这条直线的斜率．直线的斜率常用k表示，即．

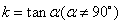　　倾斜角是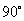的直线的斜率不存在．

　　(2)符号

　　当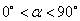时，直线的斜率是正数；

　　当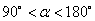时，直线的斜率是负数．

　　(3)公式

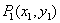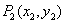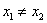　　给定两点，，且，则经过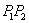的直线的斜率．

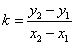　　注意：当直线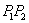与x轴平行或重合时，k=0；

　　当直线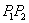与y轴平行或重合时，斜率不存在，则公式在此种情况下不适用．

3．两条直线平行的判定

　　对于两条不重合的直线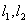，其斜率分别为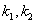．则有．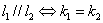

　　注意：“若两直线平行，斜率相等”的前提条件是斜率都必须存在．

4．两条直线垂直的判定

　　对于两条直线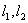，其斜率分别为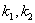．则有．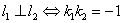

　　注意：运用此公式的前提是斜率必须存在，即两直线互相垂直，在斜率都存在的情况下有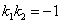，若其中一条斜率不存在，那么就不能运用这个公式．

5．直线的方程

　　(1)点斜式方程

　　直线l经过点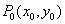，斜率为k，则可得直线l的方程为．

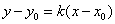　　注意：因为垂直于x轴的直线斜率不存在，故凡是垂直于x轴的直线，其方程都不能用点斜式来表示．

　　(2)斜截式方程

　　直线l的斜率为k，且与y轴的交点为（0，b），则直线l的方程为y=kx＋b．

　　直线l与y轴交点（0，b）的纵坐标b叫做直线l在y轴上的截距．

　　注意：“截距”并不是“距离”，即截距并不一定是直线与坐标轴的交点与原点的距离．而是直线与y轴交点的纵坐标．

　　(3)两点式方程

　　直线l经过两点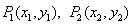（其中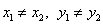），那么直线l的方程为．

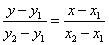　　注意：两点式方程既不能表示与x轴垂直的直线，也不能表示与y轴垂直的直线．

　　(4)截距式方程

　　直线l与x轴的交点为(a,0)，与y轴的交点为(0,b)，那么直线l的方程为．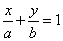

　　(5)一般式方程

　　二元一次方程Ax＋By＋c=0（A,B不同时为0）称为直线的一般式方程．

　　注意：直线的一般式方程能够表示平面上的所有直线，而点斜式、斜截式、两点式方程，都不能表示与x轴垂直的直线．

三、典型例题剖析

例1．已知过点P（）及点Q(0,b)的直线的倾斜角介于与之间，求b的范围．

[解析]

例2．直线l经过P（2,3），且在两坐标轴上截距相等，求该直线方程．

[解析]

例3．已知两直线：mx＋8y＋n=0和：2x＋my－1=0，试确定m、n的值，使

(1)；

(2)，且在y轴上的截距为－1;

(3)与相交于点P(m,－1).

[解析]

例4．点A是x轴上的动点，一条直线经过点M（2,3），垂直于MA,且交y轴于点B．过点A,B分别作x轴、y轴的垂线交于点P，求点P的坐标(x,y)满足的关系．

[解析]

例5．过点A(0,1)作一直线l，使它夹在直线：x－3y＋10=0和：2x＋y－8=0之间的线段被A点平分，求直线l的方程．

[解析]