|
一周强化
一、一周知识概述
本节主要是通过直线的方程,研究直线间的位置关系:平行和垂直,以及两条直线的交点坐标、两点间的距离公式、点到直线的距离公式等.本章自始至终贯穿数形结合的思想.在图形的研究过程中,注意代数方法的使用;在代数方法的使用过程中,加强与图形的联系.
二、重难点知识归纳
1、两条直线的交点坐标
联立两方程组成方程组并求解,若方程组有唯一解,则两条直线相交,此解就是交点的坐标;若方程组无解,则两条直线无公共点,此时两直线平行.
2、两点间的距离
对于平面任意两点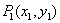 , ,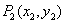 ,有 ,有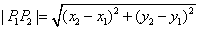 . .
3、点到直线的距离
对于任意一点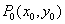 ,直线l:Ax+By+C=0. ,直线l:Ax+By+C=0.
(1)若直线l平行与x轴,即A=0,此时直线方程为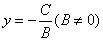 . .
点P到直线l的距离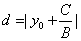 . .
(2)若直线l垂直于x轴,即B=0,此时直线方程为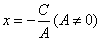 . .
点P到直线l的距离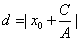
(3)若直线l既不垂直于x轴,又不平行于x轴.
点P到直线l的距离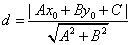 . .
三、典型例题剖析
1、直线系方程及其应用
一般地说具有某种共同属性的一类直线的集合,称为直线系.
(1)已知直线l:Ax+By+C=0,则和l平行的直线系方程为Ax+By+m=0(m为参数,m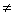 C).和l垂直的直线系方程为Bx-Ay+n=0(n为参数). C).和l垂直的直线系方程为Bx-Ay+n=0(n为参数).
(2)经过两直线交点的直线系方程为A1x+B1y+C1+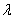 (A2x+B2y+C2)=0. (A2x+B2y+C2)=0.
例1、求经过两直线l1:x-2y+4=0和l2:x+y-2=0的交点P,并且与直线l3:3x-4y+5=0垂直的直线l的方程.
[解析]
2、利用两直线的位置关系求参数值
两直线平行或垂直时,斜率满足一定的关系利用这一关系求参数的值是一个重要的题型.
例2、已知直线l:(a-1)x+y+a+1=0及定点A(3,4),a为何值时,点A到l的距离最大?
[解析]
3、点线距离公式的应用
点线距离公式的应用较为广泛,如在求直线方程,求参数,求最值等问题中常常用到,且题型变化多,常变常新.
例3、分别过A(6,2)、B(-3,-1)两点的两条直线相平行,并且各自绕着AB旋转,如果两平行线间距离为d.
(1)求距离d的取值范围;
(2)求当d取最大值时两条直线的方程.
[解析]
4、对称问题及应用
对称问题有很多应用:光线的反射、在直线上求一点到这条直线同一侧的两点距离之和最小等等都是其对称的重要应用.
例4、已知P(2,3)和直线l:x+y+1=0.求
(1)点P关于直线l的对称点;
(2)若一束光线由P点射到l上,反射后经过点Q(1,1),求入射光线及反射光线的方程.
[解析]
5、两直线相交的问题
例5、已知两定点A(2,5),B(-2,1),直线y=x上有两动点M,N,且|MN|=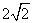 .如果直线AM与BN的交点正好落在y轴上,求M,N的坐标以及两直线AM与BN的交点C的坐标. .如果直线AM与BN的交点正好落在y轴上,求M,N的坐标以及两直线AM与BN的交点C的坐标.
[解析]
|