一周强化

一、一周知识概述

　　 本周学习了指数与指数函数，讲到了根式的概念，n次方根的基本性质.然后又学习了指数幂，规定了分数指数幂的意义以及基本运算性质，并且要简单了解无理指数幂. 在指数函数性质的学习中，要区分当底数在（0，1）和两种不同的情况时其函数值的变化，还利用了信息技术作出函数图象，并利用图象归纳函数基本性质.

二、重难点知识归纳

1．幂的概念的推广，对于指数式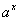来说，当指数x取各种不同的有理数时，式子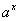的定义如下（m，n∈N，n>1）；

（1）正整数指数幂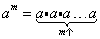

（2）零指数幂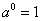：（a≠0）；

（3）负整数指数幂：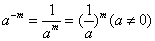

（4）分数指数幂：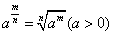

（5）无理指数幂：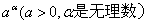

2．实数的指数幂的运算性质（其中a>0，b>0，m、n为实数）；

（1）

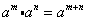
（2）

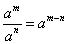
（3）

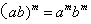
（4）

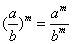
（5）

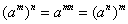
3．根式

(1)定义若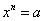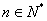（，n>1），则称x为a的n次方根(n throot)．

当n=2，n=3时，上述定义就是我们在初中学过的平方根、立方根．

若n为奇数，用符号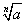表示a的n次方根，这时．

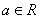若n为偶数，则要求a≥0，用符号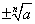表示a的n次方根．

(2)性质

①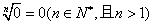

②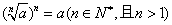

③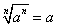（n为大于1的奇数）

④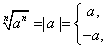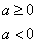（n是不等于零的偶数）

4.指数函数定义

　　一般地，函数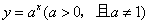叫做指数函数(exponential function)，其中x是自变量．函数的定义域是R，指数函数的值域是．

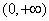5．指数函数的图象和性质

　　一般地，指数函数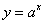在底数a>1及0<a<1这两种情况下的图象和性质如下表所示：

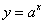
	a>1	0<a<1
图象
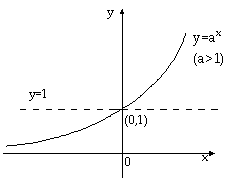
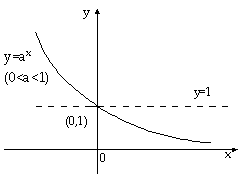
性质	（1）定义域：R
	（2）值域：（0，+∞）
	（3）过点（0，1），即x=0时,y=1
	（4）在R上是增函数	（4）在R上是减函数

6.利用函数单调性比较两实数大小，首先要通过观察分析，构造出适当的函数来，对于幂形数，若同指数不同底数，则考虑幂函数，若同底数不同指数，则考虑指数函数；其次比较大小时不仅要注意函数的单调性，还要注意幂形数比大小的两数是否都在同一函数的同一单调区间内，否则无法比较大小．

7．信息技术的使用

　　为了能够主动研究指数函数的图象和性质，可以充分利用信息技术提供的互动环境，先随意地取a的值，并在同一个平面直角坐标系内画出它们的图象，然后再通过底数a的连续动态变化展示函数图象的分布情况，这样可以更容易的概括出函数性质.

三、典型例题剖析

例1. (1)化简.

(2)计算.

[解析]

例2．若的值．

[解析]

例3．如图是指数函数（1）（2），（3）（4）的图象，则a,b,c,d与1的大小关系是（　　）

A．　　　　　　　　　　　B．

C．　　　　　　　　　　　D．

[解析]

例4．已知，求函数的最大值和最小值.

[解析]

例5．已知f(x)＝（a>0且）．

（1）求f(x)的定义域、值域．

（2）讨论f(x)的奇偶性．

（3）讨论f(x)的单调性．

[解析]