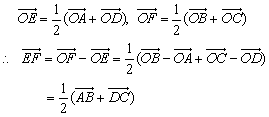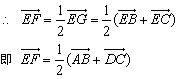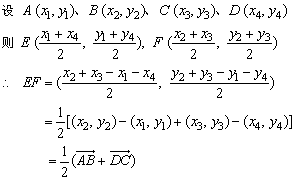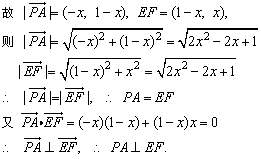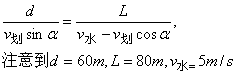|
|||
平面向量应用举例
一周强化
一、一周知识概述
向量是区别于数量的一种量,是中学数学中的一个重要概念.向量具有两重性,一是代数属性,二是几何属性,使得数与形的结合体现到极致.向量作为一种重要的数学工具,除在数学中有广泛的应用外,在物理学、工程技术中也有广泛的应用.
二、重难点知识归纳讲解
1、解决平面几何问题
由于平面向量的线性运算和数量积运算具有鲜明的几何背景,利用向量可以表示出平面几何的许多性质,如平移,平行,垂直、全等、相似以及夹角等,利用向量可以方便地解决平面几何中的一些问题,思路清晰,运算简单.
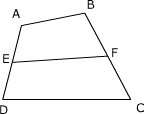
例1、已知任意凸四边形ABCD中,E、F分别是AD、BC中点,如图所示.求证:
.
解析:
向量的加法,减法的运算并不困难,但运算的途径很多,十分灵活,如平面任一向量都可以写成两个或多个向量的和.同样任一向量都可以分成两个向量的差等,本题证法较多,这里选取五种.
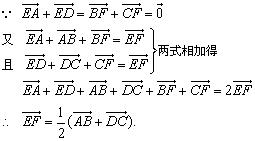
证法一:
证法二:
在平面上任取一点O,由中线公式得
证法三:
过点C在平面内作
,则四边形ABGC是平行四边形,故F为AG中点.
∴ EF是△ADG的中位线,∴ EF
DG,
∴
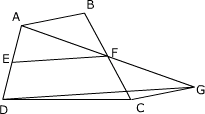
证法四:
如图所示,连EB、EC,则有
又∵ E是AD的中点,
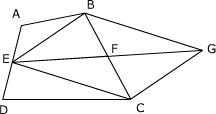
以
为邻边作平行四边形EBGC,则由F是BC之中点,可得F也是EG之中点.
证法五:
例2、如图所示,正方形ABCD中,P为线段BD上任一点,PECF为矩形,求证:
(1)PA=EF;
(2)PA⊥EF.
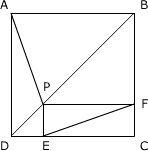
解析:平面几何问题,有的用向量的方法来处理,会有简洁的解法.此题可设坐标,利用坐标运算.
证明:以D为坐标原点,DC所在直线为x轴建立坐标系.
设C(1,0),A(0,1),P(x,x),则E(x,0),F(1,x)
2、解决函数问题
结合函数的图象,利用向量解决函数有关问题.
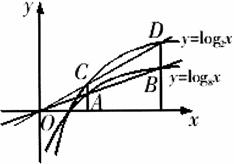
例3、过原点O的直线与函数y=log8x的图象交于A、B两点,过A、B分别作x轴的垂线交函数y=log2x的图象于C,D两点.求证:O,C,D三点在一条直线上.
分析:将共线证明转化为论证向量共线的关系式.
证明:
如图,设A(x1,log8x1),B(x2,log8x2),根据已知
共线,
∴x1log8x2-x2log8x1=0.
又根据已知C(x1,log2x1),D(x2,log2x2),
∴
∵x1log2x2-x2log2x1=x1log8x23-x2log8x13=3(x1log8x2-x2log8x1)=0,
∴
共线,即O,C,D三点在一条直线上.
三、向量在物理中的应用
运用向量解决物理问题时,必须清楚哪些物理量是向量,可以从以下几方面理解:
1、力,速度,加速度都是向量;
2、力,速度,加速度,位移的合成与分解就是向量的加减法,运动的叠加亦用到向量的合成;
3、动量
是数乘向量;
4、功定义即力
与所产生位移
的内积.
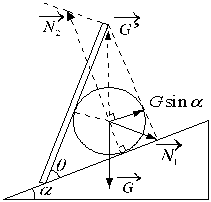
例4、如图,重力为
的均匀小球放在倾角为α的斜面上,球被与斜面夹角为θ的木板挡住,球面、木板均光滑,若使球对木板压力最小,则木板与斜面间的夹角θ应为多大?
分析:
本题可以通过把球对木板的压力N表示为关于木板夹角θ的函数,再去求N的最小值.
解:
小球受力如图:重力
,斜面弹力
(垂直于斜面),木板弹力
(垂直于木板),其中
与
合力大小恒为︱
︱,方向向上,
方向始终不变,随着木板的转动,
的大小均在变化.
=
,
当sinθ取最大值1时,︱
︱min=︱
︱sinα,此时θ=
.
点评:
对于本题的解答,要结合到物理知识即会对物理进行受力分析,才能探讨出N1与θ的函数关系式.
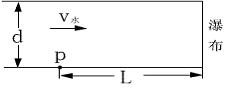
例5、今有一小船位于d=60m宽的河边P处,从这里起,在下游L=80m处河流变成“飞流直下三千尺”的瀑布.若河水流速方向由上游指向下游(与河岸平行),水速大小5m/s为,如图所示,为了小船能安全渡河,船的划速不能小于多少?当划速最小时,划速方向如何?
分析:本题可分别从数学和物理两个方面进行剖析,因而可以给出以下两种解法.
解法一:
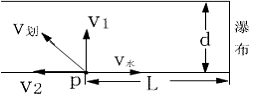
设船的划速为
,方向与上游河岸的夹角为
,如图,将
正交分解为
,
,则
船同时参与两个分运动:一个是沿
方向的速度为
的匀速直线运动,另一个是沿
方向的速度为
的匀速直线运动,这两个分运动的时间
和
必相等,设船到达对岸时,极其靠近河流与瀑布的交界处.
由
∴
令
.
显见,当
时,
有最小值为3m/s.
此时
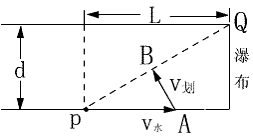
解法二:在题设条件下,船的临界合速度沿图的PQ方向,设
,从A向PQ作垂线,垂足为B,有向线段 AB即表示最小划速的大小和方向,
,
,
可见当
时,
划速方向与解法一相同.
点评:对于本题的两种解法中,分别从速度的分解与合成入手,体现了数形结合的密不可分的关系.
- 返回 -