科学探究：向心力

【学习目标】

1．知道向心力，通过实例认识向心力的作用及向心力的来源。

2．通过实验，理解向心力的大小与哪些因素有关，能运用向心力公式进行计算。

3．知道向心加速度及其公式，能用牛顿第二定律分析匀速圆周运动的向心力和向心加速度。

【学习重点】

向心力大小与m、r、ω的关系。

【学习难点】

理解向心力的概念，理解公式和。

【学习过程】

一、向心力

1．定义

做圆周运动的物体，受到的始终指向_____________的等效力。

2．方向

始终指向___________，总是与运动方向___________。

3．作用效果

向心力只改变速度__________，不改变速度_________，因此向心力________。

4．来源

可能是弹力、重力、摩擦力或是它们的合力。做匀速圆周运动的物体，向心力就是物体受到的合外力，做非匀速圆周运动的物体向心力不是物体所受到的合外力。

二、探究影响向心力大小的因素

1．实验探究（控制变量）

实验装置：向心力演示器

分组实验探究：

第一组：（1）ω、r不变，研究___________与___________关系：

用质量比为2：1的钢球和铝球，使它们运动的半径r和ω相同，观察得到露出的红白相间方格数比值为_________，即两个球所受向心力的比值也为_________，因此F与m_________。

第二组：（2）m、ω不变，研究___________与___________关系：

当m、ω相同时，半径比为2：1，向心力的比值也为_________，因此F与r_________。

第三组：（3）m、r不变，___________与___________关系：

当m、r相同，ω比值为2：1，向心力的比值为________，因此F与___________。

2．公式

F＝___________或F＝____________。

【例题】判断

（1）做匀速圆周运动的物体所受到的向心力是恒力。（×）

（2）向心力和重力、弹力、摩擦力一样，是性质力。（×）

（3）向心力是效果力，匀速圆周运动的向心力是合力，非匀速圆周运动的向心力是合力沿半径方向的分力。（√）

【思考】

自行车转弯时的运动可看作匀速圆周运动，观察下图，思考以下问题：

哪个力充当自行车转弯时的向心力？

【提示】地面静摩擦力提供自行车转弯时的向心力。

【合作探讨】

如图所示，汽车正在匀速率转弯，小球正在绳子拉力作用下做匀速圆周运动，请思考：

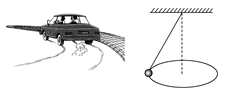
探讨（1）它们的向心力分别是由什么力提供的？

【提示】汽车转弯时的向心力由地面的静摩擦力提供，小球的向心力由重力和绳子拉力的合力提供。

探讨（2）物体做匀速圆周运动时，它所受的向心力的大小、方向有什么特点？

【提示】大小不变，方向时刻改变。

【核心点击】

3．向心力大小的计算

F_n＝mv²/r＝mrω²＝mωv＝，在匀速圆周运动中，向心力大小不变；在非匀速圆周运动中，其大小随速率v的变化而变化。

4．向心力来源的分析

物体做圆周运动时，向心力由物体所受力中沿半径方向的力提供。可以由一个力充当向心力；也可以由几个力的合力充当向心力；还可以是某个力的分力充当向心力。

【练习1】（多选）对于做匀速圆周运动的物体，下列判断正确的是（    ）

A．合力的大小不变，方向一定指向圆心

B．合力的大小不变，方向也不变

C．合力产生的效果既改变速度的方向，又改变速度的大小

D．合力产生的效果只改变速度的方向，不改变速度的大小

【解析】匀速圆周运动的合力等于向心力，由于线速度v的大小不变，故F_合只能时刻与v的方向垂直，即指向圆心，故A对，B错；由合力F_合的方向时刻与速度的方向垂直而沿切线方向无分力，故该力只改变速度的方向，不改变速度的大小，C错，D对。

【答案】AD

【练习2】用细绳拴着小球做圆锥摆运动，如图所示，下列说法正确的是（    ）

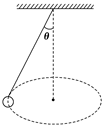
A．小球受到重力、绳子的拉力和向心力的作用

B．小球做圆周运动的向心力是重力和绳子的拉力的合力

C．向心力的大小可以表示为F＝mrω²，也可以表示为F＝mgtanθ

D．以上说法都正确

【解析】小球受两个力的作用：重力和绳子的拉力，两个力的合力提供向心力，因此有F＝mgtanθ＝mrω²。所以正确答案为B、C。

【答案】BC

【练习3】在光滑的水平面上，用长为l的细线拴一质量为m的小球，使小球以角速度ω做匀速圆周运动。下列说法中正确的是（    ）

A．l、ω不变，m越大线越易被拉断

B．m、ω不变，l越小线越易被拉断

C．m、l不变，ω越大线越易被拉断

D．m不变，l减半且角速度加倍时，线的拉力不变

【解析】在光滑的水平面上，细线对小球的拉力提供小球做圆周运动的向心力。由F＝mrω²知，在角速度ω不变时，F与小球的质量m、半径l都成正比，A正确，B错误；在质量m不变时，F与l、ω²成正比，C正确，D错误。

【答案】AC

5．向心力与合外力判断方法

（1）向心力是按力的作用效果来命名的，它不是某种确定性质的力，可以由某个力来提供，也可以由某个力的分力或几个力的合力来提供。

（2）对于匀速圆周运动，合外力提供物体做圆周运动的向心力；对于非匀速圆周运动，其合外力不指向圆心，它既要改变线速度大小，又要改变线速度方向，向心力是合外力的一个分力。

（3）无论是匀速圆周运动还是非匀速圆周运动，物体所受各力沿半径方向分量的矢量和为向心力。

（三）向心加速度

1．定义

做圆周运动的物体受到向心力的作用，存在一个由向心力产生的加速度。这个加速度叫作向心加速度。

2．大小

a＝____________＝_______________。

3．方向

向心加速度的方向时刻与________________________，且始终指向___________。

【例题】判断

（1）向心加速度只改变速度的方向，不改变速度的大小。（√）

（2）由于匀速圆周运动的速度大小不变，故向心加速度不变。（×）

（3）由于a＝ω²r，则向心加速度与半径成正比。（×）

【思考】

分析做圆周运动的物体的受力情况时，在分析了物体受其他力之后还是否再分析一个向心力？

【提示】向心力是效果力，而不是性质力，做圆周运动的物体所需要的向心力可以由一个力提供，也可以由几个力的合力或某一个力的分力提供，因此在分析物体的受力情况时，只分析性质力，不分析效果力，即不能在分析物体受其他力作用的基础上再分析物体受向心力的作用。

【合作探讨】

如图所示，自行车的大齿轮、小齿轮、后轮三个轮子的半径不一样，A、B、C是它们边缘上的三个点，请思考：

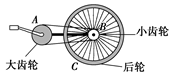
探讨（1）哪两个点的向心加速度与半径成正比？

【提示】B、C两点的向心加速度与半径成正比。

探讨（2）哪两个点的向心加速度与半径成反比？

【提示】A、B两点的向心加速度与半径成反比。

4．向心加速度的几种表达式

2．向心加速度与半径的关系

（1）若ω为常数，根据a＝ω²r可知，向心加速度与r成正比，如图甲所示。

（2）若v为常数，根据a＝v²/r可知，向心加速度与r成反比，如图乙所示。

甲                乙

（3）若无特定条件，则不能说向心加速度与r是成正比还是成反比。

【练习4】如下列选项所示，细绳的一端固定，另一端系一小球，让小球在光滑水平面内做匀速圆周运动，关于小球运动到P点时的加速度方向可能正确的是（    ）

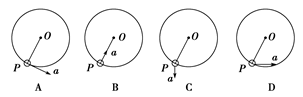
【解析】做匀速圆周运动的物体的加速度就是向心加速度，其方向指向圆心，B正确。

【答案】B

【练习5】如图所示，“旋转秋千”中的两个座椅A、B质量相等，通过相同长度的缆绳悬挂在旋转圆盘上。不考虑空气阻力的影响，当旋转圆盘绕竖直的中心轴匀速转动时，下列说法正确的是（    ）

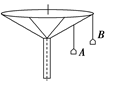
A．A的速度比B的大

B．A与B的向心加速度大小相等

C．悬挂A、B的缆绳与竖直方向的夹角相等

D．悬挂A的缆绳所受的拉力比悬挂B的小

【解析】在转动过程中，A、B两座椅的角速度相等，但由于B座椅的半径比较大，故B座椅的速度比较大，向心加速度也比较大，A、B项错误；A、B两座椅所需向心力不等，而重力相同，故缆绳与竖直方向的夹角不等，C项错误；根据F＝mω²r判断A座椅的向心力较小，所受拉力也较小，D项正确。

【答案】D

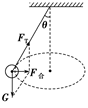
【练习6】如图所示，长为l的细线一端固定在O点，另一端拴一质量为m的小球，让小球在水平面内做角速度为ω的匀速圆周运动，细线与竖直方向成θ角，求小球运动的向心加速度。

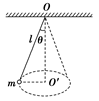
【解析】方法一：小球在水平面内做匀速圆周运动，受力分析如图所示：

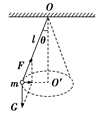
小球重力和细线拉力的合力提供小球的向心力，

根据牛顿第二定律，有，解得。

方法二：小球在水平面内做匀速圆周运动，根据向心加速度的公式，有a＝ω²r

根据几何关系，有，联立上式，解得a＝ω²。

【答案】（或ω²）

3．分析向心加速度时两点注意

（1）向心加速度的每一个公式都涉及三个物理量的变化关系，必须在某一物理量不变时分析另外两个物理量之间的关系。

（2）在比较转动物体上做圆周运动的各点的向心加速度的大小时，应先确定各点是线速度相等，还是角速度相同。在线速度相等时，向心加速度与半径成反比，在角速度相等时，向心加速度与半径成正比。

【巩固练习】

1．关于匀速圆周运动的说法，以下说法正确的是（    ）

A．因为，所以向心加速度与半径成反比

B．因为，所以向心加速度与半径成正比

C．因为，所以角速度与半径成反比

D．因为ω=2πn，所以角速度与转速成正比

2．摆角为θ的圆锥摆所受的向心力大小是（    ）

A．mg B．mgsinθ C．mgcosθ D．mgtanθ

3．如图所示，一轻杆一端固定一质量为m的小球，以另一端O为圆心，使小球在竖直面内做圆周运动。以下说法正确的是（    ）

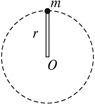A．小球过最高点时，杆受力可以是零

B．小球过最高点时的最小速率为rg

C．小球过最高点时，杆对球的作用力可以竖直向上，此时球受到的重力一定大于杆对球的作用力

D．小球过最高点时，杆对球的作用力一定竖直向下

4．关于向心力的说法正确的是（    ）

A．物体受到向心力的作用才可能做匀速圆周运动

B．向心力是指向圆心的力，是根据作用效果命名的

C．向心力可以是物体受到的几个力的合力，也可以是某个实际的力或几个力的分力

D．向心力的作用是改变物体速度的方向，不可能改变物体的速率

5．质量为m的木块从半球形的碗口下滑到碗底的过程中，如果由于摩擦力的作用使木块的速率保持不变，那么（    ）

A．因为速度大小不变，所以木块的加速度为零

B．木块下滑过程中所受的合力越来越大

C．木块下滑过程中，加速度大小不变，方向始终指向球心

D．木块下滑过程中，摩擦力大小始终不变

6．圆形轨道竖直放置，质量为m的小球经过轨道内侧最高点而不脱离轨道的最小速率为v。现在使小球以2v的速率通过轨道最高点内侧，那么它对轨道的压力大小为（    ）

A．0 B．mg C．3mg D．5mg

参考答案：

1．D

2．D

3．AC

4．ABCD

5．C

6．C