|
主讲:熊涛
一周强化
一、一周知识强化
本章要求我们掌握功率的定义,计算方法,,清楚功率是表明物体能量转化的快慢的物理量,理解功率的实际意义,掌握在题目中见到到有关功率的判断,计算等问题,特别是涉及到的两种汽车的起动问题。
二、重难点知识讲解
功率
(一)什么是功率
1、功率是做功的快慢;或单位时间内完成的功的多少。
2、定义:用物体所做的功W与完成这些功所用的时间t的比值叫功率。
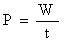
3、单位:瓦特(W),千瓦(kW)1W=1J/S
1kW=1000W1马力=735W(1马力即空调的1匹)
4、功率是标量。
功率的大小等于单位时间内力所做的功。功率是描述做功过程中能量转化快慢的物理量。
(二)额定功率与实际功率
1、额定功率:机械允许长时间正常工作时的最大功率
2、实际功率:机械实际工作时的功率
3、实际功率可以大于、等于、小于额定功率。
(三)平均功率与瞬时率
1、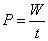 ,P代表该力在时间t内做功的平均功率。 ,P代表该力在时间t内做功的平均功率。
2、瞬时功率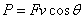
①式中F为对物体做功的力,若为发动机,则F指牵引力。
②式中v为物体的运动速度
③式中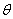 为F与v的夹角 为F与v的夹角
④若式中的v为平均速度,则P为平均功率;若式中的v为瞬时速度,则P为瞬时功率
(四)对功率的认识
1、功率是描述做功快慢的物理量
由P=W/t可知,功率的大小只与其“比值’有直接联系,与做功多少和时间长短无直接联系。比较功率的大小,要比较功与完成这些功所用时间之“比值”,“比值”大,功率就大,做功就快,“比值”小,功率就小,做功就慢。
物体做功功率是描述物体做功的一个状态;做功的多少是一个过程,所以也不能说功率大,做功就多。物体做功多少是做功物体在做功过程中的一个积累,随着做功过程的积累时间越长,这个物体做功就越多,W=Pt,t就是一个积累的意思。即P在时间t上的积累就是物体做功的多少。
2、对力的功率的认识
由P=W/t、W=Fs cosα可得,P=Fvcosα,此式中α为力F与速度v之间的夹角。把vcosα作整体来看是物体在力的方向上的分速度,即:作用在物体上的力与物体在力的方向上的分速度的乘积叫做力的功率。
对一个动力机械,当功率P一定时,由P=Fvcosα可知:降低运动速度可以增大牵引力;反过来,若阻力很小,可以加快运动速度。这一点在各种机械设备中有着广泛的应用。
任何机械都有一个标牌,标牌上所注功率为这部机械的额定功率.它是提供人们对机械进行选择、配置的一个重要参数,它反映了机械的做功能力或机械所能承担的“任务”。机械运行过程中的功率是实际功率。机械的实际功率可以小于其额定功率(称机械没吃饱),可以等于其额定功率(称满负荷运行),还可以在短时间内略大于其额定功率(称超负荷运行)。机械不能长时间处于超负荷运行,那样会损坏机械设备,缩短其使用寿命。
汽车的两种加速问题
当汽车从静止开始沿水平面加速运动时,有两种不同的加速过程,但分析时采用的基本公式都是P=Fv和F-f=ma
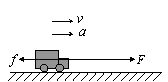
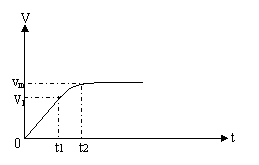
①恒定功率的加速。由公式P=Fv和F-f=ma知,由于P恒定,随着v的增大,F必将减小,a也必将减小,汽车做加速度不断减小的加速运动,直到F=f,a=0,这时v达到最大值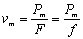 。可见恒定功率的加速一定不是匀加速。这种加速过程发动机做的功只能用W=Pt计算,不能用W=Fs计算(因为F为变力)。 。可见恒定功率的加速一定不是匀加速。这种加速过程发动机做的功只能用W=Pt计算,不能用W=Fs计算(因为F为变力)。
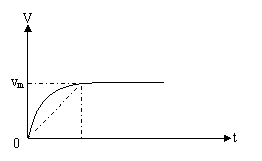
②恒定牵引力的加速。由公式P=Fv和F-f=ma知,由于F恒定,所以a恒定,汽车做匀加速运动,而随着v的增大,P也将不断增大,直到P达到额定功率Pm,功率不能再增大了。这时匀加速运动结束,其最大速度为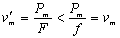 ,此后汽车要想继续加速就只能做恒定功率的变加速运动了。可见恒定牵引力的加速时功率一定不恒定。这种加速过程发动机做的功只能用W=F·s计算,不能用W=P·t计算(因为P为变功率)。 ,此后汽车要想继续加速就只能做恒定功率的变加速运动了。可见恒定牵引力的加速时功率一定不恒定。这种加速过程发动机做的功只能用W=F·s计算,不能用W=P·t计算(因为P为变功率)。
要注意两种加速运动过程的最大速度的区别。
三、典型例题
例1、将一质量为m=10 kg的物体,自水平地面由静止开始用一竖直向上的拉力F将其以a=0.5 m/s2的加速度向上拉起.
求(1)在向上拉动的10s内,拉力F做功的功率;
(2)上拉至10 s末,拉力的功率.
分析与解答:
本题的第(1)问求10 s内拉力的功率,则是指10s内的平均功率,而求平均功率有两条具体的思路:一是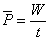 ;二是 ;二是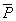 =F =F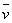 cosθ.因此本题可从这两种方法分别求出平均功率. cosθ.因此本题可从这两种方法分别求出平均功率.
方法一:
据牛顿第二定律可知,F-mg=ma,解得F=105 N.又据运动学公式可求出10 s内物体的位移为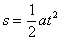 =25 m.所以有: =25 m.所以有: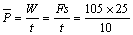 W=262.5 W. W=262.5 W.
方法二:
根据运动学公式可求出物体在10s内的平均速度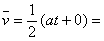 2.5 m/s,所以平均功率为: 2.5 m/s,所以平均功率为: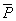 =F =F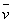 =105×2.5 W=262.5 W. =105×2.5 W=262.5 W.
对于本题的第(2)问求第10 s末的功率,即为10 s末的瞬时功率.求解瞬时功率在中学阶段只有唯一的方法:P=Fvcosθ,所以此题中10 s末的功率为:P=Fvcosθ=Fatcos0=105×0.5×10 W=525 W.
说明:
(1)由上述例题可以看出,在解题时要注意据题意分清所求功率为平均功率还是瞬时功率;(2)求解平均功率的方法较多,常见的有三种:一是利用功率的定义式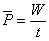 ;二是利用平均速度求解,即 ;二是利用平均速度求解,即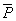 =F =F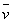 cosθ;三是利用两个状态瞬时功率的平均值法,即 cosθ;三是利用两个状态瞬时功率的平均值法,即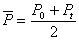 .注意:其中第二、三两种方法只适用于物体做匀变速度直线运动的情况.而求解瞬时功率在中学阶段则只有上述唯一的一种方法. .注意:其中第二、三两种方法只适用于物体做匀变速度直线运动的情况.而求解瞬时功率在中学阶段则只有上述唯一的一种方法.
例2、人的心脏每跳一次大约输送8×10-5m3的血液,正常人的血压(可看作心脏压送血液的压强)的平均值约为Q0=1.5×104Pa,心跳每分钟70次,据此估算心脏工作的平均功率为多少?
解析:
血液在心脏压力作用下沿血管流动,如图所示:
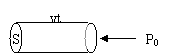
设血管橫截面积为s, 心脏平均压强为P0,
血液平均流速为v则:
由P=Fv得:P=P0sv
由题意知:svt=n Q0(n为时间内心脏跳动的次数)
联立以上两式得:P=n Q0P0/t
代入数据得:P=1.4w
例3、用100牛的力沿机械效率为60%的斜面可拉一个重400牛的物体匀速前进。据此可知斜面的高与长之比为( )
A.3∶20 B.1∶4
C.4∶1 D.20∶3
分析:
本题将机械效率知识迁移到求斜面问题上来。斜面的机械效率η=W有用/W总=(G·h)/(F·L),式中的h、L分别表示斜面的高与长。
∴h/L=η·F/G=60%·100/400=3∶20。
答案:A
说明:
机械效率是一个比值,能反映机械性能的好坏,即反映机械所完成的总功中有用功所占的比例。人们希望有用功越多越好,但事实上总不可避免要做无用功,所以人们把有用功跟总功的比值叫机械效率。
例4、物体m从倾角为α的固定的光滑斜面由静止开始下滑,斜面高为h,当物体滑至斜面底端,重力做功的瞬时功率为( )
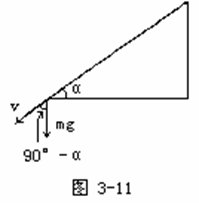
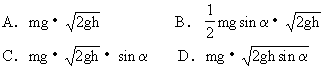
解析:
由于光滑斜面,,滑至底端时的瞬时速度为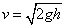 ,据瞬时功率 ,据瞬时功率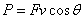 ,得F、v夹角θ为 ,得F、v夹角θ为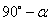
则有滑至底端瞬时功率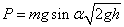
故C选项正确。
评析:
求解功率问题首先应注意求解的是瞬时值还是平均值。如果求瞬时值应注意普遍式P=Fvcosθ(θ为F,v的夹角)当F,v有夹角时,应注意从图中标明。
例5、额定功率为80kW的汽车,在某平直公路上行驶的最大速度为20m/s,汽车的质量m=2×103kg,如果汽车从静止开始做匀加速直线运动,加速度大小为2 m/s2。运动过程中阻力不变。求:
(1)汽车所受的阻力多大?
(2)匀加速直线运动的时间多长?
(3)当速度增至16m/s时,加速度多大?
解析:
(1)汽车匀加速启动过程如图所示,
当牵引力F与阻力f等大时,速度最大,功率也最大。
由P=Fv知:f=F=Pm/vm
代入数据得:f=4000N
(2)当功率达到额定值Pm时,匀加速
运动结束,此时速度为v1,牵引力为F
由牛顿第二定律得:F-f=ma 解得:F=8000N
又由P=Fv得:v1=Pm/F=10m/
由匀变速运动规律得:t1=v1/a=5 s
(3)由图知当速度增至16m/s时,正处于变加速阶段,此时功率已达到额定值Pm,由P=Fv得:F=Pm/v=5000N
由牛顿第二定律得:a=(F-f )/ m =0.5m/s2
例6、汽车在平直公路上以速度v0匀速行驶,发动机功率为P0,快进入闹市区时,司机减小了油门,使汽车的功率立即减小一半并保持该功率继续行驶。设汽车行驶过程中所受阻力大小不变,则在如图5—76所示的四个图象中,能正确表示从司机减小油门开始汽车的速度v与时间t关系的是( )
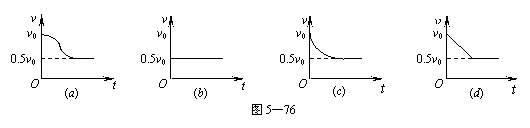
A. 图 (a) B. 图 (b)
C. 图 (c) D. 图 (d)
亮点:
汽车功率减小后的速度图象问题,要求应用功率的公式和牛顿第二定律对汽车的运动过程作具体的分析。
解析:
汽车在匀速行驶时所受阻力为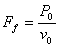 , ,
当功率减小一半时,其牵引力也相应减小一半,此时牵引力小于阻力,由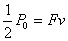 及 及 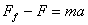 可知,随着速度的减小,F增大,进而a将减小,最终,当a=0时,速度减到最小为0.5v0,由图象斜率的意义可知,正确选项为C。 可知,随着速度的减小,F增大,进而a将减小,最终,当a=0时,速度减到最小为0.5v0,由图象斜率的意义可知,正确选项为C。
联想:
解答该类问题需要弄清两个要点:一是,汽车功率发生突变时,其运行速度不能立即突变;二是,汽车的速度、加速度、牵引力三者间的制约关系,并结合v—t图象的物理意义方可顺利得解。
例7、汽车发动机的额定功率为60kW,汽车在质量为5t,运动中所受阻力的大小恒为车重的0.1倍。
(1)若汽车以恒定功率启动,汽车所能达到的最大速度是多少?当汽车速度达5m/s时的加速度多大?
(2)若汽车以恒定加速度0.5m/s2启动。则这一过程能维持多长时间?这一过程中发动机的牵引力做功多少?
解析:
(1)汽车以额定功率起动,当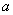 =0时的汽车速度最大。 =0时的汽车速度最大。
由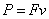 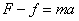 得 得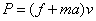
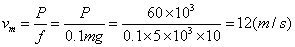
在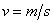 时加速度 时加速度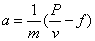
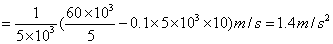
(2)汽车以0. 5m/s2加速度运动所能达到的最大速度
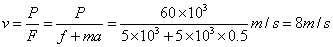
这一过程能维持的时间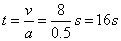
这一过程中牵引力做功
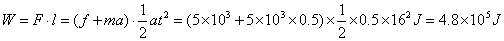
说明:
汽车起动问题常讨论两种情况:以恒定功率起动和匀加速起动。
对于汽车以恒定功率起动,要掌握两类问题的计算方法。
①由加速度求速度问题,先由牛顿第二定律求牵引力,再由P=Fv求对应的速度。
②由速度求加速度的问题,先由P=Fv求牵引力,再由牛顿第二定律求对应的加速度。
要知道a=0时汽车速度最大,可根据①的方法求最大速度。
对于汽车匀加速起动问题,要注意匀加速的末状态,功率达到额定功率,此时速度并不是汽车所能达到的最大速度,其后还有一个加速度减小的加速过程,这个过程结束时,才达到最大速度。
- 返回 -
|