1、匀速圆周运动的定义
质点沿圆周运动，如果在相等的时间内通过的弧长相等，这种运动就叫做匀速圆周运动．或者用连接圆心和质点的半径转过的角度定义：质点做圆周运动，如果连接圆心和质点的半径在相等的时间里转过的角度相等，这种运动就叫做匀速圆周运动．
2、描写匀速圆周运动的物理量
(1)线速度：圆周运动的线速度就是它的瞬时速度，匀速圆周运动物体线速度的大小，等于做匀速圆周运动的物体通过的弧长和所用时间的比值，即v=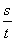
，单位：m/s．
线速度的方向沿圆周的切线，如图所示．
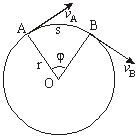
匀速圆周运动是速度大小不变的运动，而不是匀速运动，它的速度的方向时刻在变化，严格地说，应该为匀速率圆周运动．
(2)角速度：连接运动物体和圆心的半径转过的角度与所用时间的比值，叫做匀速圆周运动的角速度，即ω=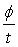
，单位为：弧度/秒，符号是rad/s．
可见：匀速圆周运动是角速度不变的圆周运动．
(3)周期：做匀速圆周运动的物体运动一周所用的时间叫周期，周期用T表示，单位为秒(s)．
周期描写了匀速圆周运动的一个重要特点——时间周期性．其具体含意是，描写匀速圆周运动的一些变化的物理量，每经过一个周期时，大小和方向与初始时刻完全相同．例如线速度以及下节课要讲的向心加速度等．
(4)转速和频率：单位时间内质点转过的圈数，叫做转速，常用符号n表示，单位符号是r/s或r/min，读作转每秒或者转每分；单位时间内完成完整圆周运动的次数叫做频率，用f表示，单位是赫兹，符号是Hz．显然，当单位时间取1s时，f=n．
3、描写匀速圆周运动的各物理量之间的关系
(1)线速度与角速度的关系：在v=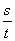
中取t=T(1个周期的时间)，则s=2πr，所以v=
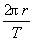；在ω=
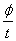中，取t=T，则φ=2π，所以ω=
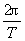，比较可见v=ωr，这个重要的关系也可以由v=
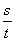，s=rφ推出，即v=
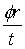=ωr．这个关系的意义是线速度的大小等于角速度与半径的乘积．
(2)角速度、周期、频率、转速间的关系
ω=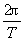
=2πf=2πn(n为r/s)．
解决匀速圆周运动问题的方法：
①明确质点匀速圆周运动的圆心和半径；
②寻找各物理量之间的联系，灵活选取公式进行计算
4、对圆周运动角速度和线速度关系的理解
（1）匀速圆周运动是一种重复性的运动，即是一种周期性的运动，周期性运动的快慢仅用已经学过的线速度的大小是不能准确表达的．定义了角速度ω=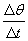
之后，便可以肯定地说，角速度越大，物体转过一周用的时间(即周期T)就越小，这种周期性运动就越快．物体运动的角速度ω、周期T、频率f、转速n都能表达匀速圆周运动这种周期性运动的快慢．它们之间的联系是：ω=2πf=
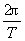=2πn
(2)在半径r一定的情况下线速度v∝ω，即角速度越大时线速度正比增大，在这种情况下线速度也能描述匀速圆周运动的快慢．
(3)当ω一定时，线速度v∝r，圆周半径大的质点线速度大，此种情况线速度便不能描述此周期性运动的快慢．
(4)当线速度v一定时，ω∝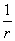
，即半径越小，角速度越大，完成一个周期性运动用的时间越短．
5、线速度的方向以及线速度方向变化的快慢
(1)匀速圆周运动的物体线速度的方向时刻在变化，但总是与圆周相切、与半径垂直．
(2)物体做圆周运动的半径转过多少度，线速度的方向就改变多少度．角速度ω越大，半径在单位时间内转过的角度也越大，速度方向改变的角度也越大，所以，角速度越大，圆周运动的线速度方向改变就越快．
6、灵活地运用数学知识：如圆心角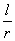θ=
，Δθ=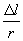
，2π弧度等于360°，圆周的切线总是与半径垂直等．
7、对一些典型现象的理解：皮带传动的两个轮子边缘上点的线速度大小相等，转动的物体上(如地球上)，不同的点具有相同的角速度等．
例1、机械表的时针和分针做圆周运动
A．分针的角速度是时针角速度的12倍
B．分针的角速度是时针角速度的60倍
C．如果分针的长度是时针长度的1．5倍，则分针端点的线速度是时针端点线速度的18倍
D．秒针的角速度是分针的60倍
思路：(1)将机械表的时、分、秒针视为匀速转动的物体，将针上的一点视为做匀速圆周运动的质点，比较三个针在相同的时间内转过的角度，由角速度的定义ω=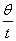
可获得结论．
(2)根据角速度和线速度的关系v=ωr比较分针与时针上不同点的线速度的大小．
答案：ACD
例2、如图所示，A、B两个齿轮的齿数分别是z1、z2，各自固定在过O1、O2的轴上．其中过O1的轴与电动机相连接，此轴每分钟转速为n1．若两齿轮外缘半径分别是r1、r2，求：
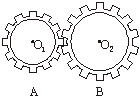
(1)B齿轮的转速n2；
(2)A、B两齿轮的半径之比；
(3)在时间t内，A、B两齿轮转过的角度之比，以及B齿轮外缘上一点通过的路程．
思路：在齿轮传动装置中，各齿轮的“齿”是相同的，齿轮的齿数对应齿轮的周长．在齿轮传动进行转速变换时，单位时间内每个齿轮转过的齿数相等，相当于每个接合的齿轮边缘处线速度大小相等，因此齿轮传动满足的关系是齿轮转速与齿数成反比，即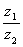
=
=
．
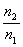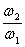答案：(1)n2=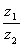
n1 (2)r1∶r2=z1∶z2 (3)sB=2πr2n1tz1/z2
例3、求地球表面上北纬60°处的物体随地球自转而做匀速圆周运动的线速度是多大?这个速度的参考系是什么?这个速度随纬度的变化如何变化?
解析：求地球北纬60°处物体的线速度，首先需要确定物体做匀速圆周运动的半径r，要确定半径r就必须找出物体做匀速圆周运动的圆心．其二，要明确物体做匀速圆周运动的角速度ω，然后由v=ωr可求物体的线速度的大小．如图所示，物体做匀速圆周运动的平面是过北纬60°与地轴垂直的平面，圆心是平面与地轴的交点O′，设地球的半径为R，则物体做匀速圆周运动的半径为r=Rcos60°，根据ω=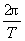
知，物体绕地轴转动的角速度ω自=
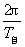，物体线速度的大小v=ω自r=
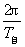Rcos60°．地球的自转周期T自=24 h，地球半径R≈6400 km，统一单位后代入上式可求v的大小为232.5 m/s．
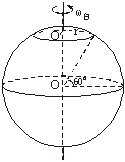
物体绕地轴自转线速度的参考系是地轴．这个线速度v=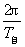
Rcosθ，随纬度增大，θ增大，线速度变小．当θ=90°，即物体在两极时，物体的线速度为零．
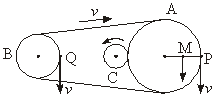
例4、如图所示是生产流水线上的皮带传输装置，传输带上等间距地放着很多半成品产品．A轮处装有光电计数器，它可以记录通过A处的产品数目．已知测得轮A、B的半径分别为rA=20 cm，rB=10 cm，相邻两产品距离为30 cm，1 min内有41个产品通过A处．求：
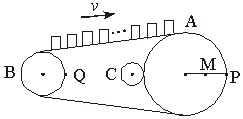
(1)产品随传输带移动的速度大小；
(2)A、B轮轮缘上的两点P、Q及A轮半径中点M的线速度和角速度大小，并在图中画出线速度方向；
(3)如果A轮是通过摩擦带动C轮转动，且rC=5 cm，在图中描出C轮的转动方向，求出C轮的角速度(假设轮不打滑)．
解析：首先明确产品与传送带保持相对静止的条件下，产品速度的大小就等于传送带上每一点速度的大小，在传送带不打滑的条件下，传送带上各点运动速度的大小都等于A、B轮缘上点的线速度的大小．由传送带相邻产品的间距及单位时间内通过A处的产品的个数可以确定出皮带上点的速度，进而知道A、B轮缘上的两点P、Q线速度的大小，然后由线速度与角速度的关系，求出A、B两轮的角速度及A轮半径中点M的线速度及C轮的角速度．由题意知，1分钟内有41个产品通过A处，说明1分钟内传输带上每点运动的路程为两产品间距的40倍．设传输带运动速度大小为v，则
(1)v=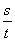
=
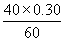m/s=0．2 m/s．
(2)vP=vQ=0．2 m/s．A轮半径上的M点与P点的角速度相等，故
vM=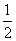
vP=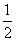
×0．2 m/s=0．1 m/s
ωP=ωM=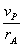
=
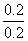rad/s=1 rad/s，ωQ=2ωP=2 rad/s．
(3)C轮的转动方向如图所示，如果两轮间不打滑，则它们的接触处是相对静止的，即它们轮缘的线速度大小是相等的，所以ωCrC=ωArA．
C轮的角速度ωC=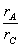
ωA=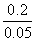
·1 rad/s=4 rad/s．
点评：本题旨在考查学生对传动装置中各物理量的联系的理解，并能熟练地运用匀速圆周运动的规律解决问题．
答案：
(1)0．2 m/s
(2)vP=vQ=0．2 m/s vM=0．1 m/s ωP=1 rad/s ωQ=2 rad/s
(3)ωC=4 rad/s
