1、分式方程
分母中含有未知数的方程叫做分式方程．如：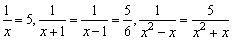
等等都是分式方程．
在此之前我们学过的方程，分母中都不含有未知数，都是整式方程，因此目前学过的方程可归纳为：
2、解分式方程的基本思路——转化
解分式方程的基本思路是将分式方程转化为整式方程．这种转化的具体做法是“去分母”，即方程两边同乘最简公分母，归纳如下：
如：解方程：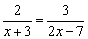
方程两边都乘以(x＋3)(2x－7)得
2(2x－7)=3(x＋3)
4x－14=3x＋9
x=23
3、解分式方程的一般步骤
（1）去分母：方程两边同乘以各分母的最简公分母，将分式方程转化整式方程．
（2）解整式方程．
（3）验根，即把整式方程的根代入最简公分母，看结果是不是零，若结果不是零，说明此根是原方程的根；若结果是零，说明此根是原方程的增根，必须舍去．见例1．
（4）写出方程的解．
解分式方程的一般步骤列表如下：
例1、解下列分式方程：
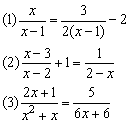
分析：
（1）先确定最简公分母为2(x－1)，再按步骤求解．
（2）先将2－x化为－(x－2)，然后去分母求解．
（3）先将分母分解因式，再确定公分母为6x(x＋1)．
解：
（1）方程两边同乘以2(x－1)，得
2x=3－4(x－1)
解之得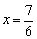
检验：当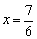
时，2(x－1)
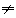0
∴
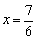是原方程的根．
（2）方程两边同乘以(x－2)，得
x－3＋(x－2)=－1
2x－5=－1
解之得x=2
检验：将x=2代入最简公分母x－2=0，
∴x=2为原方程的增根．
∴原方程无解．
（3）原方程可变为：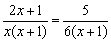
方程两边同乘以6x(x＋1)，得
12x＋6=5x
解之得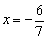
检验：将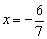
代入最简公分母
∴
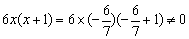
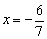是原方程的解．
例2、甲乙两地相距150千米，一轮船从甲地逆流航行至乙地，然后又从乙地返回甲地，已知水流速度为3千米/时，回来时所用时间是过去的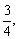
求轮船在静水中的速度．
分析：
本题的基本量之间的关系有：路程=速度×时间，v逆=v静－v水，v顺=v静＋v水，本题的等量关系为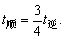
解：
设轮船在静水中的速度为x千米/时
则v逆=(x－3)千米/时，v顺=(x＋3)千米/时
根据题意得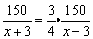
解之得x=21
经检验，x=21是所列方程的解．
答：船在静水中的速度是21千米/时．
例3、甲、乙两个工程队共同完成一项工程，乙队先单独做一天后，再由两队合作2天，就完成了全部工程．已知甲队单独完成工作所需的天数是乙队单独完成所需天数的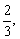
求甲、乙两队单独完成各需多少天？
分析：本题是研究甲、乙两队的工程问题，他们单独工作的工作量、工作效率、工作时间列表如下：
相等关系：
乙做一天的工作量＋甲、乙合作2天的工作量=1
解：
设乙单独完成工程需x天，那么甲单独完成需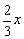
天．
则根据题意，得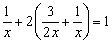
即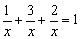
解得x=6 经检验，x=6是原方程的根．
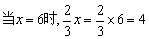
答：甲、乙两队单独完成分别需要4天和6天．
例4、解下列关于字母x的方程：
(1)m2(x－n)=n2(x－m)(m2≠n2)
(2)ay－bx=1(ab≠0)
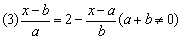
分析：
这三个方程中，x是未知数，其他字母都是已知数，其步骤与解数字系数的方程相同，在最后系数化1时，注意字母的取值范围．
解：
（1）去括号，m2x－m2n=n2x－n2m
m2x－n2x=m2n－mn2
(m2－n2)x=mn(m－n)
∵m2≠n2,∴m2－n2≠0
∴方程两边同除以(m2－n2)
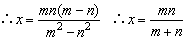
(2)由ay－bx=1得
ay－1=bx
∵ab≠0, ∴a≠0且b≠0
∴方程两边同除以b，得
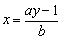
（3）去分母：b(x－b)=2ab－a(x－a)
bx－b2=2ab－ax＋a2
bx＋ax=b2＋2ab＋a2
(b＋a)x=(a＋b)2
∵a＋b≠0
∴方程两边同除以a＋b，
得 x=a＋b
例5、解方程：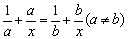
解法一：方程两边同乘以abx得
bx＋a2b=ax＋ab2
bx－ax=ab2－a2b
(b－a)x=ab(b－a)
∵a≠b，∴a－b≠0
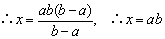
检验：将x=ab代入原方程
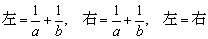
∴x=ab为原方程的解．
解法二：由原方程得：
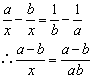
方程两边同乘以abx
ab(a－b)=(a－b)x
∵a≠b ，∴a－b≠0
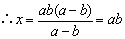
例6、分别求出下列公式中的未知量：
（1）在公式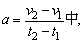
求t2(a≠0)．
（2）在公式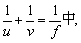
求u(f≠v)．
分析：
求公式中的某一个量，这个量就是未知数，其余量均为已知数．
解：
（1）去分母：a(t2－t1)=v2－v1
at2－at1=v2－v1
at2=at1＋v2－v1
∵a≠0,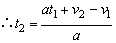 
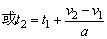
（2）去分母：vf＋uf=uv
uf－uv=－vf
u(f－v)=－vf
∵f≠v, ∴f－v≠0
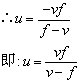
例7、解方程：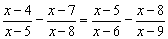
解法一：
原方程可化为：
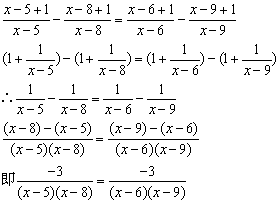
去分母，得－3(x－6)(x－9)=－3(x－5)(x－8)
即(x－6)(x－9)=(x－5)(x－8)
∴x2－15x＋54=x2－13x＋40
－2x=－14，∴x=7
将x=7代入方程，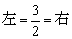
∴x=7是原方程的根．
解法二：直接通分
原方程可化为：
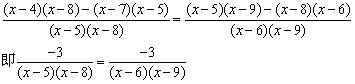
去分母，得(x－6)(x－9)=(x－5)(x－8)
解之得x=7
将x=7代入(x－5)(x－8) (x－6)(x－9)≠0
∴x=7是原方程的根．
例8、编一道可化为一元一次方程的分式方程的应用题，并解答，编写要求：
（1）要联系实际生活，其解符合实际．
（2）根据题意列出的分式方程只含有两项分式，不含常数项，分式的分母均含有未知数，并且可化为一元一次方程．
（3）题目完整，题意清楚．
分析：
本题着重从三步考虑：
①依题意，确定一个有意义的数字．
如5，当作所列应用题方程的一个根，建立一个题设要求的等式：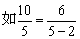
②把上述等式中的5用未知数x代替，变等式方程为分式方程．即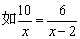
③根据方程编出应用题．
甲、乙二人做某种机器零件，已知甲每小时比乙多做2个，甲做10个所用的时间与乙做6个所用时间相等．求甲、乙每小时各做多少个？
解：
设甲每小时做x个，则乙每小时做(x－2)个，
根据题意，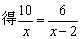
整理，得10x－20=6x，∴x=5
经检验，x=5是所列方程的根．
答：甲每小时做5个，乙每小时做3个．
说明：
（1）本题考查列分式方程解应用题和编应用题的逆向思维能力．题目属于开放性问题，答案不唯一．
（2）解此类题的关键是先找好等量关系，确定出相等的式子，如本例中的：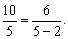
由此式，再去确定问题情景，也可用于下列问题．
甲、乙二人步行去某地，甲的速度比乙的速度快2千米/时，又知甲步行10千米与乙步行6千米的时间相同，求甲、乙二人的速度各是多少？
例9、一个分数，如果分子加1就变为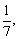
如果分母加1就变为
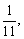求这个分数．
解：
设这个分数的分子为x，分母为y．
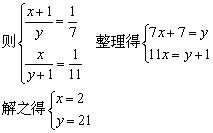
经检验，x=2，y=21是方程组的根，因此这个分数是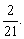
例10、某自来水公司水费计算办法如下：若每户每月用水不超过5m3，则每立方米收费1.5元，若每户每月用水超过5m3．则超出部分每立方米收取较高的的定额费用，1月份，张家用水量是李家用水量的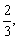
张家当月水费是17.5元，李家当月水费是27.5元，问超出5m3的部分每立方米收费多少元？
分析：
列分式方程解应用题关键是找出相等关系，分析出数量关系，从而恰当地设未知数、列方程、写解答、检验．此题的主要等量关系是：1月份张家用水量是李家用水量的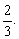
即1月份张家用水量=李家用水量的
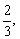所以首先要表示出1月份张家用水量和李家用水量，而用水量可以用水费除以水的单价得出，只不过计算时要将水费分成两部分：5m3内的水费与超出5m3部分的水费．
解：
设超出5m3部分的水，每立方米收费x元，则1月份，张家超出5m3部分的水费为(17.5－1.5×5)元，超出5m3的用水量为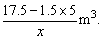
李家超出5m3部分的水费为(27.5－1.5×5)元，超出5m3的用水量为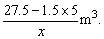
根据题意，得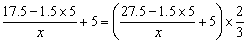
解这个方程，得x=2．
经检验，x=2是所列方程的根且符合题意．
答：超出5m3部分的水，每立方米收费2元．
