主讲：陈逸

一周强化

一、一周知识概述

1、分式

一般地，如果A、B表示两个整式，并且B中含有字母，那么式子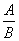叫做分式．

分式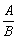中，A叫做分子，B叫做分母．

2、分式有意义、无意义，分式的值为零的条件

分式有意义的条件是分式的分母不为0；

分式无意义的条件是分式的分母为0；

分式的值为0的条件是分子为0，且分母不为0．

3、分式的基本性质

　　分式的分子与分母同乘(或除)以一个不为零的整式，分式的值不变．用式子表示为：

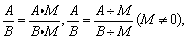　　其中A、B、M为整式．

4、约分

　　与分数的约分类似，利用分式的基本性质，约去分式的分子和分母的公因式，不改变分式的值，这样的分式变形叫做分式的约分．

5、分式的乘除法法则

　　分式乘分式，用分子的积作积的分子，分母的积作积的分母；

　　分式除以分式，把除式的分子、分母颠倒位置后与被除式相乘．

　　

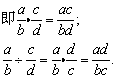
6、同分母的分式的加减法

　　同分母的分式相加减，分母不变，把分子相加减．

　　即．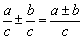

7、通分

　　与分数通分类似，利用分式的基本性质，使分式的分子分母同乘以适当的整式，不改变分式的值，化异分母分式为同分母分式，这样的分式变形叫做分式的通分．

8、异分母分式加减法

　　异分母分式相加减，先通分，变为同分母分式，然后再加减．

　　即．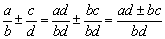

二、重难点知识归纳

1、重点：分式的四则运算顺序：先乘除，后加减．同级运算中，从左到右．在乘除运算中，一般先化除法运算为乘法运算．加减法运算中，先化异分母为同分母，再进行计算．

2、难点：分式的加、减、乘、除运算是一种混合运算，除了四则运算的顺序外，还得具体问题具体分析．如：计算：这是一道异分母的加减法运算。若一开始就将三个异分母通分，这就很麻烦，显然，应将前两项先通分计算然后再与第三项计算就简便多了．另外，分母、分子是多项式的还应先分解因式，再找最简公分母，这个部分应加强练习．

三、典型例题剖析

例1、使得分式有意义的条件是（　）

A．x≠0　　　　　　　　　　　B．x≠－1且x≠－2

C．x≠－1　　　　　　　　　　D．x≠－1且x≠0

[解析]

例2、当x为何值时，分式，

（1）有意义；（2）值为零．

[解析]

例3、已知．

[解析]

例4、计算：

　　

　　．

[解析]

例5、计算

[解析]

- 返回 -