1、二元一次方程
（1）含有两个未知数，并且所含未知数的项的最高次数是1的方程，叫做二元一次方程．
（2）二元一次方程的一般形式：
ax＋by=c (a、b、c均为已知数，且ab≠0）
2、二元一次方程组
（1）把由两个一次方程组成，且含有两个未知数的方程组，叫做二元一次方程组．
（2）二元一次方程组通常可写成：
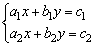（a1，b1，c1，a2，b2，c2均为已知数，且a1b2≠a2b1）
3、二元一次方程组的解
二元一次方程组的两个方程的公共解，叫做二元一次方程组的解．
4、二元一次方程组解法的基本思想
二元一次方程组中有两个未知数，如果消去其中一个未知数，将二元一次方程组转化为一元一次方程，就可以先解出一个未知数，然后再设法求另一个未知数，这种将未知数的个数由多化少，逐一简化的思想方法，叫做消元思想.
即二元一次方程组
形如：ax=b（a，b为已知数）的方程.
5、代入消元法
由方程组中一个方程，将一个未知数用含另一未知数的式子表示出来，再代入另一方程，实现消元，进而求得这个二元一次方程的解，这种方法叫做代入消元法，简称代入法.
6、用代入消元法解二元一次方程组的步骤
（1）从方程组中选取一个系数比较简单的方程，把其中的某一个未知数用含另一个未知数的代数式表示出来.
（2）把（1）中所得的方程代入另一个方程，消去一个未知数.
（3）解所得到的一元一次方程，求得一个未知数的值.
（4）把所求得的一个未知数的值代入（1）中求得的方程，求出另一个未知数的值，从而确定方程组的解.
7、加减消元法
两个二元一次方程中同一个未知数的系数相反或相等时，将两个方程的两边分别相加或相减，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法，简称加减法.
8、加减消元法解二元一次方程组的一般步骤
（1）把一个方程或者两个方程的两边乘以适当的数，使方程组的两个方程中一个未知数的系数互为相反数或相等；
（2）把两个方程的两边分别相加或相减，消去一个未知数，得到一个一元一次方程；
（3）解这个一元一次方程，求得一个未知数的值；
（4）把求得的未知数的值代入到原方程组中的系数比较简单的一个方程中，求出另一个未知数的值；
（5）把求出的未知数的值写成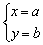
的形式.
9、二元一次方程组解的情况
若二元一次方程组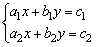
（a1，a2，b1，b2，c1，c2均为不等于0的已知数），则
（1）当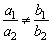
时，这个方程组只有唯一解；
（2）当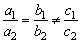
时，这个方程组无解；
（3）当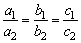
时，这个方程组有无穷多个解.
②
③
是它的一个解，那么a的值为_____．．
乙因抄错c，解得
求a、b、c的值．
与方程组
有相同的解，求a、b 的值.
当m为何值时，方程组有惟一解？无解？有无数组解？
，
的值.