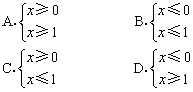
（2）已知不等式组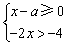
有解，则a的取值范围为（ ）
A．a＞－2 B．a≥－2
C．a＜2 D．a≥2
（3）若不等式组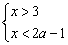
无解，则a的取值范围是（ ）
A．a≤2 B．a<3
C．a>3 D．a≥3
分析：
（1）数轴上表示的不等式的解集分别是x≥0和x≥1；
（2）由于不等式组的解集为a≤x<2，则去掉不等式中间的x，显然a＜2.
（3）由于不等式组无解，所以两不等式的解集没有公共部分.
∴2a－1≤3. 即a≤2.
答案：（1）A； （2）C； （3）A
例2、已知x，y的方程组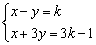
的解满足
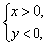求k的取值范围.
分析：
先求出方程组的解，再依条件列出不等式组，解这个不等式组即得k 的取值范围.
解答：
解方程组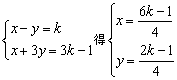
又∵x>0, y<0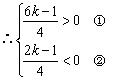 
由①得6k－1>0，即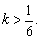
由②得2k－1<0，即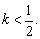
∴k的取值范围是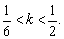
例3、某服装厂现有A种布料70m，B种布料52m. 现计划用这两种布料生产M、N两种型号的时装共80套，已知做一套M型号时装需A种布料0.6m，B种布料0.9m，可获利润45元；做一套N型号时装需用A种布料1.1m、B种布料0.4m，可获利润50元. 请你设计最佳方案.
分析：
从题目所提供的信息知，最佳方案是指：如何安排生产M、N两种型号的时装，使得所获利润最大，并且所需A种布料不多于70m，B种布料不多于52m，因此我们将问题转化为一元一次不等式组的问题来求解.
解：
设生产N型号的时装套数为x，用这批布料生产这两种型号的时装所获的总利润为y元，根据题意可得：
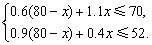
解得40≤x≤44.
∵x为整数
∴x的取值可为40，41，42，43，44.
又y=45(80－x)＋50x=5x＋3600.
显然，x的值越大，y的值也越大.
∴当x=44，y有最大值为5×44＋3600=3820.
即：当N型号时装生产44套时，所获利润最大，最大利润是3820元.
例4、黄冈启黄中学七年级（2）班有若干名学生住宿，若每间住4人，则有20人没宿舍住；若每间住8人，则有一间宿舍住不满，求住宿学生的人数及宿舍的间数.
分析：
此题存在的等量关系为：住宿学生的人数=宿舍的间数×4＋20；
存在的不等量关系为：0＜最后一间宿舍的人数＜8.
解：
设该校有x间宿舍，住宿的学生有y人.
依题意，得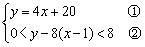
由①代②，得0＜4x＋20－8(x－1)<8
即0＜28－4x<8，解得5<x＜7.
∵房间数x取正整数，∴x=6.
y=4x＋20=44.
答：住宿学生人数为44人，宿舍的间数为6间.
例5、在车站开始检票时，有a(a>0)名旅客在侯车室排队等候检票进站，检票开始后，仍有旅客继续前来排队检票进站，设旅客按固定的速度增加，检票口检票的速度也是固定的.若开放一个检票口，则需30分钟才可将排队等候检票的旅客全部检票完毕；若开放两个检票口，则只需10分钟便可将排队等候的旅客全部检票完毕；如果要在5分钟内将排队等候检票的旅客全部检票完毕，以使后来到站的旅客能随到随检，至少要同时开放几个检票口？
分析：
此题已知的常量只有三个时间，未知的量确有四个：字母a；每分钟新增加的旅客的人数x；检票口每分钟检票的人数y；所要求开放的检票口n.题中含有的相等关系或不等关系有：
开放一个检票口时，存在等量关系a＋30x=30y；开放两个检票口时，存在等量关系a＋10x=2·10y；5分钟检票完毕时，存在不等关系a＋5x≤n·5y．
先由两个相等关系式求出x，y，再利用不等关系式求出n的范围，根据a>0，n为正整数来确定n的值.
解：
设检票开始后每分钟新增加的旅客为x人，检票的速度为每个检票口每分钟检y人，5分钟内检票完毕要同时开放n个检票口.
根据题意，得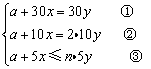
②×3－①，得2a=30y，得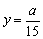
，④
把④代入①，得
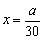，⑤
把④⑤代入③，得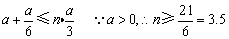
n取最小的整数，∴n=4.
答：至少需要同时开放4个检票口.
