一周强化

一、一周内容概述

　　线段的定比分点坐标公式是向量坐标运算的应用之一，是把有向线段和分点所具有的图形特征，通过坐标运算表示出来．通过本节学习，要正确理解P分有向线段所成的比λ的含义，掌握有向线段的定比分点坐标公式和线段的中点坐标公式，并能熟练运用公式解决实际问题．

　　平面向量的数量积是平面向量这一章重点内容之一，其难点是数量积定义的正确理解，以及运算律的证明与正确使用．通过本节的学习，使同学们知道数量积是向量之间的乘法，与数的乘法是有区别的，故实数乘法的有关运算律不能照搬施行于向量乘法.

二、重点知识归纳

（一）线段定比分点的意义

　　设P1、P2是直线上的两点，点P是上不同于P1、P2的任意一点，若，则称点P为有向线段的分点，λ为分点P分线段所成的比．

（二）λ取值范围与点P的位置之间的关系

λ＞0时P在线段P1P2上　　　　　　　　　　

－1＜λ＜0时，P在反向延长线上　　　

λ＜－1时，P在的延长线上　　　　　　

（三）内分点与外分点的定义

若分点P在有向线段内，则称分点P为内分点；

若分点P在有向线段外，则称分点P为外分点．

（四）分点坐标公式：

若P(x，y)，P1(x1，y1)，P2(x2，y2)，

（五）中点坐标公式：

若P(x，y)是P1(x1，y1)，P2(x2，y2)的中点，则

（六）数量积及相关概念

向量的夹角	如图所示，已知两个非零向量a和b，作则∠AOB=θ（0°≤θ≤180°）叫作向量a和b的夹角.当a、b同向时，θ=0°；当a、b异向时，θ=180°.
数量积的定义	已知两个非零向量a和b，它们的夹角为θ，则数量|a|·|b| cosθ 叫做a和b的数量积（内积），记作a·b，即a·b=|a|·|b|cosθ.
数量积的几何意义	数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积.

（七）数量积的重要性质

设a、b都是非零向量，e是单位向量，θ是a与e的夹角，根据定义可推得如下性质.

（1）e·a=a·e=|a|cosθ.

（2）当a与b同向时，a·b=|a|·|b|；当a与b反向时，a·b=－|a|·|b|.特别地，a·a=|a|2，或.

（3）当a⊥b时，a·b=0；反之也成立，即a⊥ba·b=0.

（4）（向量夹角的公式）.

（5）|a·b|≤|a|·|b|.

（八）向量数量积的运算律

交换律	a·b = b·a
与实数相乘的结合律	（λa）·b =λ（a·b）= a·λb
分配律	（a＋b）·c= a·c＋b·c

（九）向量垂直的充要条件

向量式	a⊥ba·b=0
坐标式

三、难点知识剖析

（一）在运用线段的定比分点坐标公式时，要注意(x1，y1)是起点的坐标，(x2，y2)是终点的坐标，(x，y)表示分点的坐标，在每个等式中涉及到四个不同的量，它们分别表示三个坐标和定比λ，只要知道其中任意三个量，便可求第四个量．

（二）如何确定定比分点坐标公式中的λ

　　1、由坐标确定：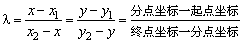

　　2、由（不能错误的表示为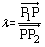）再据的方向决定λ的符号．

（三）特殊情况的分析

1、λ＝0时，分点P与起点P1重合

2、λ＝1时，分点P为线段P1P2的中点

3、λ不可能等于－1（若λ＝－1，则P1、P2重合，与P1P2为线段矛盾）

　　∴λ∈(－∞，－1)∪(－1，＋∞)

4、无论λ取何实数（当然λ≠－1）分点P不可能与终点P2重合

（四）关于平面向量的数量积的定义及几何意义，要注意：

　　（1）两个向量的数量积是两个向量之间的一种乘法，与以前学过的数的乘法是有区别的，在书写时一定要把它们严格区分开来，决不可混淆. a·b中的点“·”一般不能省略.

　　（2）在运用数量积公式解题时，一定要注意两向量夹角范围是0°≤θ≤180°.

　　（3）当a≠0时，由a·b =0不能推出b一定是零向量，这是因为任意一个与a垂直的非零向量b，都有a·b =0.这由向量的几何意义就可以理解.

（五）向量的数量积的性质有

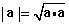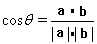，，a·b=0a⊥b，

因此，用平面向量的数量积可以解决有关长度、角度、垂直的问题.

（六）关于向量数量积的运算性质，要注意：

　　（1）二向量的数量积不是向量而是数量.要准确区分二向量数量积的运算性质与数乘向量、实数与实数的积之间的差异.

　　（2）若a、b、c（b≠0）为实数，则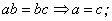但对于向量就不正确，即.

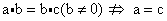　　（3）数量积的运算只适合交换律、加乘分配律及数乘结合律，但不适合乘法结合律，即（a·b）c不一定等于a（b·c）.这是由于（a·b）c表示一个与c共线的向量，而 a（b·c）表示一个与a共线的向量，而c与a不一定共线.也就有a（b·c）与（a·b）c不一定相等.

四、例题讲解

例1、已知点A分有向线段的比为2，求下列定比λ：

（1）A分的比；

（2）B分的比；

（3）C分的比．

[解析]

例2、已知三点A(x1，y1)，B(x2，y2)，C(x3，y3)，D点内分的比为，E在BC上，且使△BDE的面积是△ABC面积的一半，求向量的坐标．（提示：三角形面积等于两边与其夹角正弦乘积的一半）

[解析]

例3、若直线y＝－ax－2与连接P(－2，1)、Q(3，2)两点的线段有交点，求实数a的取值范围．

[解析]

例4、已知：|a|=3，|b|=6，当①a∥b，②a⊥b，③a与b的夹角是60°时，分别求a·b.

[解析]

例5、已知a、b都是非零向量，且a＋3b与7a－5b垂直，a－4b与7a－2b垂直，求a与b的夹角.

[解析]

例6、如图，在△ABC中，AB=AC，D是BC的中点，E是从D作AC的垂线的垂足，F是DE的中点.求证：AF⊥BE.

[解析]