三角形用符号“△”表示，顶点是A、B、C的三角形记作△ABC，读作“三角形ABC”．
（2）三角形的分类
三角形按边可以分成如下两类：
（3）三角形的三边的关系
①三角形的任意两边之和大于第三边，
②三角形的任意两边之差小于第三边．
即三角形的三边为a,b,c，则a+b>c，b+c>a，c+a>b;
a－b＜c，b－c＜a，c－a＜b
三角形的边的不等关系的应用和作用：
①判断三条线段a、b、c能否组成三角形，其判断方法有如下三种：
1°当a＋b>c，b＋c>a，c＋a>b都成立，即三条边都小于其它两条边之和时，能组成三角形；
2°当|a－b|<c<a＋b时，即任意一条边大于其它两条边差的绝对值（即大边减小边），而小于其它两条边之和，可以构成三角形；
3°当a最长，且有b＋c>a时，即最大边小于其它两条边之和时可以构成三角形．
②确定三角形第三边的取值范围：
两边之差的绝对值＜第三边＜两边之和
如果三角形已知两边分别为a、b，第三边为c，则|a－b|<c<a＋b
从而得到三角形的周长的取值范围，设a>b，则2a<a＋b＋c<2(a＋b)
③说明线段的不等关系．
例1、已知：△ABC的周长是12cm，且三角形的三边是连续的整数，求三角形三条边的长．
分析：
要求三角形的边长，由△ABC的周长是12，可建立方程来求解．
解答：
设三角形三边的长分别为x，(x＋1)和(x＋2)，依题意可列方程：
x＋(x＋1)＋(x＋2)=12，解得x=3．
故三角形的三边长分别为3cm、4cm和5cm．
例2、有木条4根，长度分别是12cm，10cm，8cm，4cm，选其中三根组成三角形，能组成三角形的个数是（ ）
A．1 B．2 C．3 D．4
分析：
解决本题须分二步进行，首先把4根木条选三根分成四组，然后判断每组能否构成三角形．
解答：
4根木条按三根为一组可分如下四组：
12cm，10cm和8cm；12cm，10cm和4cm；
10cm，8cm和4cm；12cm，8cm和4cm．
由三角形三边关系定理及推论知：
12<10＋8，则12cm，10cm和8cm能构成三角形．
12<10＋4，则12cm，10cm和4cm能构成三角形．
10<8＋4，则10cm，8cm和4cm能构成三角形．
答案：C
例3、已知：三角形两边的长分别为2cm和7cm，第三边长的数值是偶数，求这个三角形的周长．
分析：已知两边的长可判断第三边的取值范围．
解答：
设第三边的长为xcm，根据三角形的三边关系有：7－2<x<7＋2，即5<x<9．
∵x为偶数，∴x=6或8．
故三角形的周长为15cm或17cm．
例4、如图，P是△ABC内一点，试说明AB＋AC>PB＋PC成立的理由．
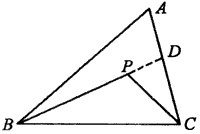
分析：
三角形三边关系可以用来说明线段之间的不等关系，但题目中涉及的线段不在同一个三角形中，所以需要添加辅助线，构造新的三角形．比较明显的辅助线可以作BP或CP的延长线．
解答：延长BP交AC于D，
在△ABD中，AB＋AD>BD，
即AB＋AD>BP＋PD．
在△PCD中，PD＋CD>PC．
两式相加，得AB＋AD＋PD＋CD＞BP＋PD＋PC，
∴AB＋AC＋PD>PB＋PC＋PD，
即AB＋AC>PB＋PC．
2、三角形的高
从三角形的一个顶点向它的对边所在的直线画垂线，顶点和垂足间的 线段叫做三角形的高线，简称三角形的高．如图，从△ABC的顶点A向它所对的边BC所在的直线画垂线，垂足为D．那么线段AD叫△ABC的边BC上的高．
三角形的高的数学语言：
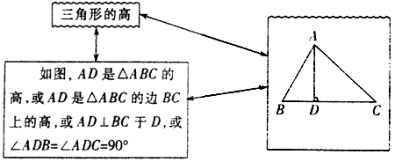
三角形的三条高相交于一点，这一点叫三角形的垂心．
例5、如图，是甲、乙、丙、丁四位同学画的钝角△ABC的高BE，其中画错的是_________．
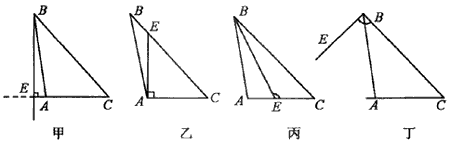
分析：
甲图错在把三角形的高线与AC边的垂线定义混淆，把“线段”画成“直线”；
乙图错在没有过点B画AC的垂线，故不是AC边上的高；
丙图错在未抓住“垂线”这一特征，画出的BE与AC不垂直；
丁图错在没有向点B的对边画垂线．
解答：甲、乙、丙、丁．
例6、不等边△ABC的两边高分别为4和12，若第三边上的高也是整数，试求它的长．
分析：
由两边的高4和12可以求出这两边的关系，从而可以表示出第三边的取值范围，再用面积法可以求出第三边上的高．
解答：
设三角形三边为a、b、c，第三边上的高为h，则有
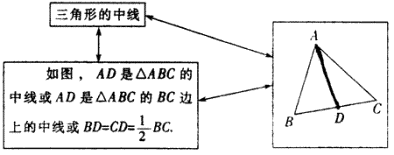
3、三角形的中线
在三角形中，连接一个顶点和它对边中点的线段叫做三角形的中线．如图，连接△ABC的顶点A和它所对的边BC的中点D，所得线段AD叫做△ABC的边BC上的中线．
一个三角形有三条中线，并且都在三角形的内部，它们相交于一点，这一点叫三角形的重心．
三角形中线的数学语言：
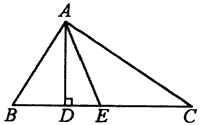
例7、如图，已知AD、AE分别是△ABC的高和中线，AB=6cm，AC=8cm，BC=10cm，∠CAB=90°，试求：（1）AD的长；（2）△ABE的面积；（3）△ACE和△ABE周长的差．
分析：
直角三角形的面积等于两直角边的积的一半，又等于斜边与斜边上的高的积的一半；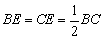
，所以△ABE的面积是△ABC的面积的一半；△AEC的周长与△ABE的周长的差为：AC＋EC＋AE－（AB＋BE＋AE）=AC－AB．
解答：
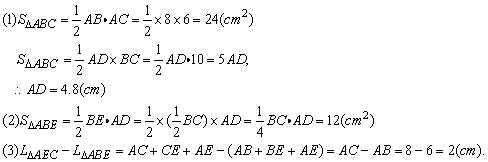
4、三角形的角平分线
在三角形中，一个内角的平分线与对边相交，这个顶点与交点之间的线段叫做三角形的角平分线．如图，∠A的平分线与对边BC交于点D，那么线段AD叫做三角形的角平分线．
一个三角形有三条角平分线，并且都在三角形的内部，它们相交于一点，这一点叫做三角形的内心．
三角形角平分线的数学语言：
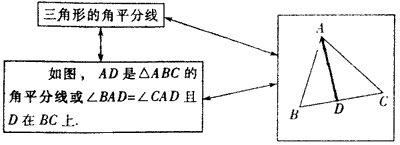
例8、如图，若AD是△ABC的角平分线，DE//AB.
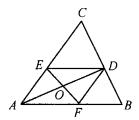
（1）若DF//AC，EF交AD于点O．试问：DO是否为△EDF的角平分线？并说明理由；
（2）若DO是△EDF的角平分线，试探索DF与AC的位置关系，并说明理由．
分析：
（1）要判断DO是否为△EDF的角平分线，即要判断∠EDA与∠ADF是否相等；
（2）由DO是△EDF的角平分线知∠EDA=∠ADF，由DE//AB，AD平分∠CAB得∠EAD=∠ADF．
解：
（1）DO是△DEF的角平分线，理由如下：
由DE//AB，得∠EDA=∠DAF．由DF//AC，得∠EAD=∠ADF．
又AD是△ABC的角平分线，有∠EAD=∠DAF．所以∠EDA=∠ADF．
（2）DF//AC．理由如下：
∵DO是△EDF的角平分线，∴∠EDA=∠ADF，又DE//AB，∴∠EDA=∠DAF．
∵AD平分∠CAB，∴∠EAD=∠DAF．
∴∠EAD=∠ADF，∴DF//AC．
5、三角形的稳定性
用三根长度适当的木条，用钉子把它们钉成一个三角形框架，所得到的框架形状和大小就固定了，三角形的这个性质称为三角形的稳定性．
例9、如图，是一个六边形木架，那么至少需加钉几根木条才能固定该六边形木架呢？
分析：
由于三角形具有稳定性，而其他的图形则不具有稳定性．因此要确定至少需要几根木条才能固定六边形框架，只需确定该六边形能分割成几个互不重叠的三角形．
解：至少需要3根木条．
