主讲：陈逸

一周强化

一、一周知识概述

1、分式方程

　　分母中含有未知数的方程叫做分式方程．如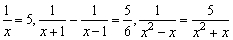：等等都是分式方程．

　　在此之前我们学过的方程，分母中都不含有未知数，都是整式方程，因此目前学过的方程可归纳为：

　　

2、解分式方程的基本思路——转化

　　解分式方程的基本思路是将分式方程转化为整式方程．这种转化的具体做法是“去分母”，即方程两边同乘最简公分母，归纳如下：

　　．

3、解分式方程的一般步骤

　　（1）去分母：方程两边同乘以各分母的最简公分母，将分式方程转化整式方程．

　　（2）解整式方程．

　　（3）验根，即把整式方程的根代入最简公分母，看结果是不是零，若结果不是零，说明此根是原方程的根；若结果是零，说明此根是原方程的增根，必须舍去．

　　（4）写出方程的解．

　　解分式方程的一般步骤列表如下：

4、列分式方程解应用题的步骤

　　（1）审清题意，找出题目的等量关系，设出未知数．

　　（2）根据等量关系，列出分式方程．

　　（3）解分式方程，并验根．

　　（4）写出答案．

二、重难点知识归纳

1、重点

　　①可化为一元一次方程的分式方程的解法步骤；

　　②验根的必要性；

　　③分式方程在实际生活中的应用．

2、难点

　　①为什么要验证根及如何验根；

　　②应用题中如何设未知数，找等量关系．

三、典型例题剖析

例1、解下列分式方程

　　（1）；

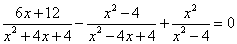　　（2）；

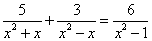　　（3）当m为何值时，关于x的方程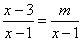产生增根．

[解析]

例2、甲乙两地相距150千米，一轮船从甲地逆流航行至乙地，然后又从乙地返回甲地，已知水流速度为3千米/时，回来时所用时间是过去的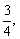求轮船在静水中的速度．

[解析]

例3、某文具店出售每册为120元和80元的两种纪念册，两种纪念册都有30%的利润，但每册120元的不好出售。某人身带1080元，想买120元纪念册若干，但看价格表摇头，因为钱不够，当经理了解了该买主的意图后，仍然如数付给这个顾客，仍获得和卖出相同数量的每册80元的纪念册的利润一样多，买主满意而归，经理得意而笑，请问，这个买主共买了多少册？

[解析]

例4、解下列关于字母x的方程：

(1)m2(x－n)=n2(x－m)(m2≠n2)

(2)ay－bx=1(ab≠0)

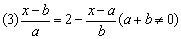
[解析]

例5、解方程：．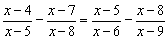

[解析]

例6、某自来水公司水费计算办法如下：若每户每月用水不超过5m3，则每立方米收费1.5元，若每户每月用水超过5m3．则超出部分每立方米收取较高的定额费用，1月份，张家用水量是李家用水量的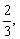张家当月水费是17.5元，李家当月水费是27.5元，问超出5m3的部分每立方米收费多少元？

[解析]

- 返回 -