|
主讲: 高级教师
程金菊
一周强化
一、一周知识概述
(一)多边形有关概念
1、多边形定义:在平面内,由不共线的一些线段首尾顺次相接组成的图形叫做多边形,组成多边形的线段,叫做多边形的边,多边形中相邻两边组成的角叫做它的内角,多边形的边与它的邻边的延长线组成的角叫做外角.
2、多边形按其组成图形的线段的条数分类,一个多边形由n条线段构成,那么这个多边形就叫做n边形.
3、凸多边形
画出多边形的任何一条边所在的直线,如果多边形都在这条直线的同侧,那么这个多边形就是凸多边形.今后我们研究的多边形都是凸多边形.
(二)正多边形
1、如果多边形的各内角都相等,各边也都相等,那就称它为正多边形.
2、连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
一个n边形从一个顶点出发的对角线的条数为(n-3)条,其所有的对角线为 条. 条.
(三)多边形内角和定理
n边形的内角和等于(n-2)·180°(n≥3的正整数),可见多边形内角和与边数n有关,每增加1条边,内角和增加180°.
(四)多边形外角和定理
1、多边形外角和定义:在多边形的每个顶点处取多边形的一个外角,它们的和叫做多边形的外角和.
2、多边形外角和定理:任意多边形的外角和等于360°.
注意:n边形的外角和恒等于360°,它与边数的多少无关.
(五)平面镶嵌
1、用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌。
2、用相同的正多边形铺地板.
对于给定的某种正多边形,它能否拼成一个平面图形,而不留一点空隙?显然问题的关键在于分析能用于完整铺平地面的正多边形的内角特点.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角360°时,就铺成一个平面图形.
事实上,正n边形的每一个内角为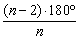 ,要求k个正n边形各有一个内角拼于一点,恰好覆盖地面,这样360°= ,要求k个正n边形各有一个内角拼于一点,恰好覆盖地面,这样360°=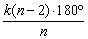 ,由此导出 ,由此导出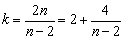 ,而k是正整数,所以n只可能为3,4,6.因此,用相同的正多边形地板砖铺地面,只有正三角形,正四边形,正六边形的地砖可以用. ,而k是正整数,所以n只可能为3,4,6.因此,用相同的正多边形地板砖铺地面,只有正三角形,正四边形,正六边形的地砖可以用.
我们知道,任意四边形的内角和都等于360°.所以用一批形状大小完全相同但不规则的四边形瓷砖也可以铺成无空隙的地板.用任意相同的三角形可以铺满地面吗?请同学们拼拼看.
3、用两种或两种以上的正多边形拼地板
我们已知知道.有些相同的正多边形能够铺满地面,而有些则不行.实际上我们还看到有不少用两种以上边长相等的正多边形组合成的平面图案.如教材上所列的几种情况.为什么这些正多边形组合能够密铺地面?这个问题实质上是相关正多边形“交接处各角之和能否拼成周角”的问题.
二、重难点知识归纳
(一)多边形内角和定理的证明
1、在n边形内任取一点,并把这点与各顶点连结起来,共构成n个三角形,这n个三角形的内角和为 n·180°,再减去一个周角,即得到多边形的内角和为(n-2)·180°.
2、过n边形一个顶点连对角线,可以得(n-3)条对角线,并且将n边形分成(n-2)个三角形,这(n-2)个三角形的内角和恰好是多边形的内角和,等于(n-2)·180°.
3、在n边形一边上取一点与各顶点相连,得(n-1)个三角形,n边形内角和等于这(n-1)个三角形内角和减去所取点处的一个平角,即(n-1)·180°-180°=(n-2)·180°.
注意:以上各推导方法体现将多边形问题转化为三角形问题来解决的基本思想.
(二)多边形外角和定理的证明
多边形的每个内角与它相邻的外角是邻补角,所以n边形内角和加外角和等于n·180°,外角和等于n·180°-(n-2)·180°=360°.
(三)多边形边数与内角和、外角和的关系
1、内角和与边数成正比,边数增加,内角和增加;边数减少,内角和减少.每增加一条边,内角和就增加180°.(反过来也成立)
2、多边形外角和恒等于360°,与边数的多少无关.
(四)多边形最多有三个内角为锐角,最少没有锐角(如矩形);多边形的外角中最多有三个钝角,最少没有钝角.
(五)多边形在实际生活中有着广泛应用
多边形在实际生活的应用很广泛,如公园里铺的地板砖,这些砖的设计,都要用到多边形的内角.但并不是所有多边形都可用来整齐地铺地,用来铺地的多边形必须满足同顶点的所有角的和等于360°.
三、典型例题讲解
例1、已知两个多边形的内角和的和为1980°,且这两个多边形的边数之比为2∶3,求这两个多边形的边数.
[解析]
例2、一个凸多边形,除了一个内角外,其余各内角的和为2750°,求这个多边形的边数以及除去一个内角的度数.
[解析]
例3、一个多边形,除了一个内角之外,其余各内角和为2750°,求这个多边形对角线的条数.
[解析]
例4、足球一般是由许多黑白相同的小皮缝合而成的,黑块呈五边形,白块呈六边形(如图所示).已知黑块有12块,则白块有_____________.

[解析]
例5、任何一个凸多边形的内角中,为什么不能有3个以上的锐角.
[解析]
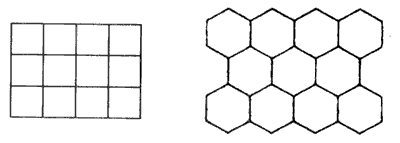
例6、我们经常见到如图那样的地面,它们分别是全用正方形或全用正六边形材料铺成的,这样形状的材料能铺成平整、无空隙的地面.
现在,问:
(1)像上面那样铺地面,能否全用正五边形的材料?
(2)你能不能另外想出一个有一种多边形(不一定是正多边形)的材料镶嵌平面的方案?把你想到的方案画成草图.
(3)请你再画一个用两种不同的正多边形材料镶嵌平面的草图.
[解析] - 返回 -
|