主讲：方敏文

一周强化

一、一周知识概述

1、轴对称图形

　　一般地，如果一个图形沿某条直线对折后，直线两旁的部分能够完全重合，那么这个图形就叫做轴对称图形，这条直线叫做对称轴．

2、两个图形成轴对称

　　如果两个图形沿着一条直线对折后，这两个图形完全重合，我们就说这两个图形成轴对称，这条直线叫做对称轴，两个图形中的对应点(即对折后两图形中互相重合的点)叫做对称点．

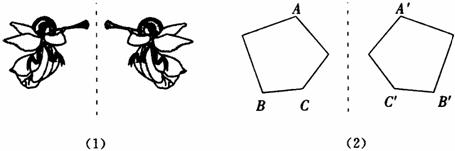
　　如下图(1)所示，两个图形关于虚线成轴对称．

　　如下图(2)所示，点A的对称点是A′，点B′，C′分别是点B，C的对称点．

3、线段的垂直平分线

　　我们把垂直并且平分一条线段的直线称为这条线段的垂直平分线，又叫中垂线．

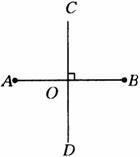
　　例如：如图所示，点O是线段AB的中点，且AB⊥CD，垂足为点O．

4、线段垂直平分线的性质

　　（1）线段垂直平分线上的点与这条线段两个端点的距离相等．

　　（2）与一条线段两个端点距离相等的点，在这条线段的垂直平分线上．

5、角平分线的性质

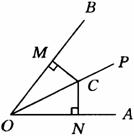
　　角的平分线上的点到这个角的两边的距离相等．如图所示，射线OP是∠AOB的平分线，点C在射线OP上，CM⊥OB，CN⊥OA，垂足分别为点M，N，则CM=CN．

6、轴对称的性质

　　如果两个图形关于某一条直线对称，那么①对应线段相等，②对应角相等，③对应点所连的线段被对称轴垂直平分．

7、对称轴的画法

　　如果一个图形是轴对称图形，那么连结对称点的线段的垂直平分线就是该图形的对称轴．

二、重难点知识概述

1、两个图形成轴对称是指两个图形之间的形状与位置关系，包含两层意思：

　　①有两个图形，形状大小完全相同；

　　②重合的方式有限制，即它们的位置必须满足一个条件：把它们沿某一条直线折叠后能够完全重合．

2、轴对称图形与两个图形成轴对称的区别与联系：

　　区别：①轴对称是两个图形的对称关系，轴对称图形是一个图形自身的对称特征；

　　②两个图形成轴对称的对称点分别在两个图形上，轴对称图形的对称点都在同一个图形上；

　　③两个图形成轴对称，其对称轴可能在两个图形的外部，也可能经过两个图形的内部或它们的公共边（点），轴对称图形的对称轴一定经过这个图形的内部．

　　联系：①都是沿着某直线对折后能够互相重合；

　　②如果把轴对称的两个图形看作一个整体，那么它就是一个轴对称图形；如果把轴对称图形沿对称轴分成两部分，那么这两部分就是关于这条对称轴对称．

3、线段的垂直平分线说明了垂直平分线与线段的两种关系：①是位置关系——垂直；②是数量关系——平分．

4、对称轴是轴对称图形的任何一对对应点所连线段的垂直平分线，包含如下两层含义：

　　①已知一对对应点就能作出它们的对称轴；

　　②已知一点和对称轴就能作出该点关于对称轴的对称点．

三、典型例题剖析

例1、左边图形与右边图形成轴对称的是(　)

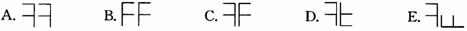
分析：

　　两个图形关于某直线成轴对称图形，就是看沿某直线对折后，两个图形是否完全重合．由上图可知，C正确．

例2、如图所示，正三角形有三条对称轴，正方形有四条对称轴，正五边形有五条对称轴，请画出下列图形的所有对称轴，猜测正六边形的对称轴的个数，画出图形，正n边形有多少条对称轴？

分析：

　　如下图所示，正三角形、正方形和正五边形的对称轴如下：

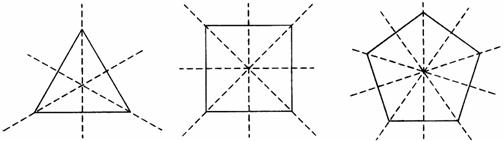
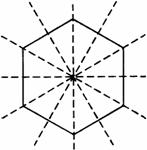
　　猜测正六边形的时称轴有6条，如下图所示，正n边形有n条对称轴．

例3、在下图中，分别作出点P关于OA，OB的对称点P1，P2，连接P1、P2交OA于M，交OB于N，若P1P2=5cm，则△PMN的周长为多少？

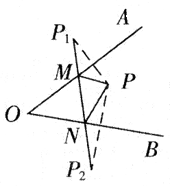
分析：

　　求△PMN的周长即是求PM＋PN＋MN．因为P，P1关于OA对称，P，P2关于OB对称，所以PM=P1M，PN=P2N，因而PM＋PN＋MN＝P1M＋MN＋P2N．

解：

　　∵P1是P关于OA的对称点，P2是P关于OB的对称点，

　　∴PM=P1M，PN=P2N，

　　∴PM＋PN＋MN＝P1M＋MN＋P2N＝P1P2＝5cm，

　　∴△PMN的周长是5cm．

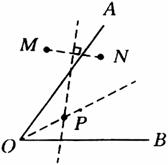
例4、如下图所示，有两个班的学生分别在M、N两处参加植树劳动，现要在道路OA，OB的交叉区域内设一个茶水供应站P，使P到两条道路的距离相等，且PM=PN，有一个同学说：“只要作一个角的平分线和一条线段的垂直平分线，这个茶水站的位置就确定了．”你认为这位同学说得对吗？如果对，请画出图形，找到这个位置；如果不对，请说明理由．

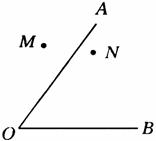
分析：

　　设点P到OA，OB的距离相等，则这个点在∠AOB的平分线上，又由PM=PN，则点P在线段AB的垂直平分线上，因此点P在线段MN的垂直平分线与∠AOB的平分线的交点上．

解：

　　这位同学说得对，点P的位置如图0所示．

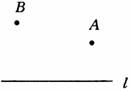
例5、如图所示，牧童在A处放牛，他的家在B处，晚上回家时要到河边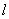让牛饮一次水，则饮水的地点选在何处，牧童所走的路最短？

分析：

　　本题A，B两点在河的同侧，直接确定牛饮水的位置并不容易，但若A，B在河的两侧就容易了．本题可利用轴对称的性质将A点转化到河流的另一侧，设为A′，不论饮水处在什么位置，A点与它的对称点到饮水处的距离都相等．当A′B最小时，饮水处到A，B的距离和最小．

解：如图所示，点C即为所求．

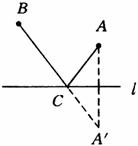
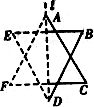
例6、如图，给出了一个图案的一半，其中虚线l是这个图案的对称轴，请画出这个图形的另一半，并说出这个图案的形状.

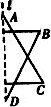
分析：

　　正确找出点B，点C关于l为对称轴的对称点是画出另一半图形的关键.

解答：

　　如图中虚线所示，这个图案是一个六角星.

- 返回 -