|
主讲:陈逸
一周强化
一、一周知识概述
1、一次函数的概念
一般地,如果两个变量x与y之间的函数关系,可以表示为y=kx+b(k、b为常数,且k≠0)的形式,那么称y是x的一次函数.
特别地,当b=0时,y叫做x的正比例函数.
2、一次函数的图象
(1)一次函数y=kx+b(k≠0)的图象是经过(0,b)和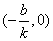 两点的一条直线,因此一次函数y=kx+b的图象也称为直线y=kx+b. 两点的一条直线,因此一次函数y=kx+b的图象也称为直线y=kx+b.
(2)一次函数y=kx+b的图象的画法.
根据几何知识:经过两点能画出一条直线,并且只能画出一条直线,即两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线即可.一般情况下:是先选取它与两坐标轴的交点:(0,b), .即横坐标或纵坐标为0的点. .即横坐标或纵坐标为0的点.
3、一次函数的性质
| |
b>0 |
b<0 |
b=0 |
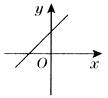
k>0 |
经过第一、二、三象限 |
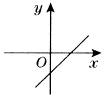
经过第一、三、四象限 |
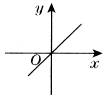
经过第一、三象限 |
|
|
|
图象从左到右上升,y随x的增大而增大 |
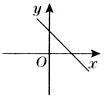
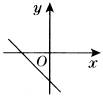
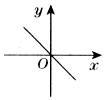
k<0 |
经过第一、二、四象限 |
经过第二、三、四象限 |
经过第二、四象限 |
|
|
|
图象从左到右下降,y随x的增大而减小 |
4、一次函数y=kx+b(k、b为常数,且k≠0),当b=0时,一次函数就成为y=kx(k≠0),则称y是x的正比例函数.因此正比例函数是一次函数的特殊情形.
函数 |
图象 |
性质 |
y=kx(k≠0) |
k>0 |
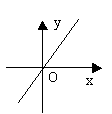
|
①过原点(0,0)
②过第一、三象限
③y随x的增大而增大 |
k<0 |
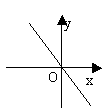
|
①过原点(0,0)
②过第二、四象限
③y随x的增大而减小 |
5、用待定系数法确定函数关系式的一般步骤:
(1)根据已知条件写出含有待定系数的函数关系式;
(2)将x、y的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程;
(3)解方程得出未知系数的值;
(4)将求出的待定系数代回所求的函数关系式中.
二、重难点知识归纳
1、在y=kx+b(k≠0)中,一定要考虑x的取值范围,即在自变量x的取值范围内,对于每一个确定的x的值,一定有唯一确定的值与它对应.对于实际应用问题,画图象时,还要注意应用问题中自变量的取值范围,准确而灵活画图象.
2、一次函数y=kx+b(k≠0)的图象是一条直线,由于两点确定一条直线,因此,通常选取直线与两坐标轴交点,即直线y=kx+b是经过(0,b)和(-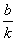 ,0)的一直线,而正比例函数y=kx(k≠0)的图象是经过(0,0)和(1,k)的一条直线. ,0)的一直线,而正比例函数y=kx(k≠0)的图象是经过(0,0)和(1,k)的一条直线.
三、典型例题剖析
例1、已知函数 ,m为何值时,函数是正比例函数? ,m为何值时,函数是正比例函数?
解析:因为y是x的正比例函数,
所以
所以当m=2时,y是x的正比例函数.
点拨:正比例函数应满足自变量指数为1、自变量的系数不为零.
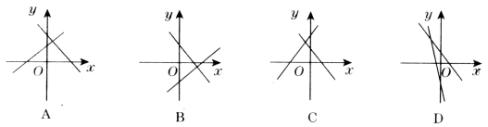
例2、两个一次函数y1=mx+n,y2=nx+m,它们在同一坐标系中的图象可能是图中的( )
分析:
若m>0,n>0,则两函数图象都应经过第一、二、三象限,故A、C错,若m<0,n>0,则y1=mx+n的函数图象过第一、二、四象限,而函数y2=nx+m的图象过第一、三、四象限,故D错.若m>0,n<0,y1=mx+n的图象过第一、三、四象限,函数y2=nx+m的图象过第一、二、四象限,故选B.
答案:B
例3、已知一次函数y=kx+b的图象经过点(0,2)和点(1,-1),求:
(1)这个一次函数的关系式;
(2)在直角坐标系中画出它的图象.
解析:
(1)∵一次函数y=kx+b的图象经过点(0,2)和点(1,-1),则 . .
∴ ,故所求的一次函数关系式为 y=-3x+2. ,故所求的一次函数关系式为 y=-3x+2.
(2)一次函数 y=-3x+2的图象是经过(0,2)和(1,-1)的一条直线,如图所示:
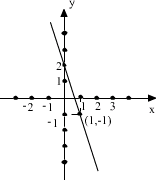
例4、某地长途汽车客运公司规定旅客可以随身携带一定重量的行李,如果超过规定,则需购买行李票,行李票费用y(元)是行李重量x(公斤)的一次函数,其图像如图所示.求:(1)y与x之间的函数关系式;(2)旅客最多可免费携带行李多少公斤?
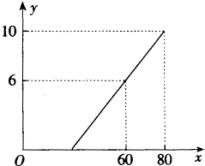
分析:
由所给的图像可知x=60和x=80时,所对应的y值分别是6和10,通过方程组可求出y与x之间的函数关系式.得到关系式后,由y=0.求得的x值即是最多可免费携带行李的公斤数.
解:
(1)设一次函数的关系式为y=kx+b.
因为当x=60时,y=6;当x=80时,y=10,
所以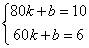 ,解得 ,解得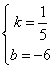 . .
所以所求函数关系式是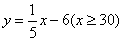 . .
(2)当y=0时,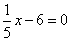 ,所以x=30. ,所以x=30.
所以旅客最多可免费携带30公斤行李.
点拨:在实际问题中,求得关系式后应注明自变量的取值范围.
例5、已知一次函数y1=ax+b,y2=cx+5,学生甲发现当x=3时,y1=y2=-2,学生乙因不小心把c看错了,而解得:当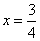 时, 时, .请问:你能根据以上的信息,写出这两个一次函数正确的关系式吗? .请问:你能根据以上的信息,写出这两个一次函数正确的关系式吗?
解析:
显然由学生甲的解答知:当x=3时, ,∴ ,∴ . .
∴解得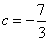 ,∴ ,∴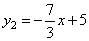 为正确的一次函数关系式, 为正确的一次函数关系式,
又学生乙没看错系数a与b,∴当 时, 时,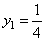 , ,
∴ ,∴解方程组 ,∴解方程组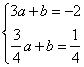 ,得a=-1,b=1. ,得a=-1,b=1.
∴正确的关系式为y1=-x+1与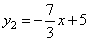 . .
- 返回 -
|