本周学习有理数的乘法、除法和乘方，以及科学记数法、近似数和有效数字．
（一）、有理数乘法的法则及运算律
1、有理数的乘法法则
两数相乘，同号得正，异号得负，并把绝对值相乘；任何数同零相乘，都得零.
几个不等于零的数相乘，积的符号由负因数的个数决定，当负因数有奇数个时，积为负；当负因数有偶数个时，积为正.几个数相乘，有一因数为零，积就为零. 两个有理数的积等于1，这两个数互为倒数.
2、运算定律
（1）乘法交换律：两个数相乘，交换因数的位置，积不变.即ab=ba.
（2）乘法结合律：三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积不变.
（3）乘法分配律：一个数与两个数的和相乘，等于把这个数分别与两个数相乘，再把积相加.即a(b＋c)=ab＋ac.
（二）、有理数的除法法则
1、有理数的除法法则
法则1：除以一个数等于乘以这个数的倒数，0不能作除数；
法则2：两数相除，同号得正，异号得负，并把绝对值相除，零除以任何一个不等于零的数都得零．
2、倒数的意义
乘积是1的两个数互为倒数，其中一个数是另一个数的倒数，0没有倒数.
（三）有理数乘方法则：正数的任何次幂都是正数；负数的奇次幂是负数，负数的偶次幂是正数，零的任何非零次幂都是零．
（三）、科学记数法
一个大于10的数可以记为a×10n的形式，其中a是整数数位只有一位的数，即1≤a＜10，n是正整数，像这样的记数法就是科学记数法．
注意：用科学记数法表示大于10的有理数时，n是比原数的整数数位少1的整数．
（四）近似数和有效数字
1、近似数：近似数就是与实际很接近的数．取近似数的方法是“四舍五入法”，还有根据实际问题而采用的“进一法”和“去尾法”．
2、有效数字：一般地，一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位．这时，从左边第一个不是0的数字起，到末位数字为止，所有的数字都叫做这个数的有效数字．
对带有计数单位的近似数，其有效数字的确定由记数单位前的数字确定．如28.70万有4个有效数字2、8、7、0，而不是6个．
用科学记数法表示的近似数，其有效数字由a×10n（1≤a＜10）中的a确定，如1.350×104中有4有效数字1、3、5、0．
3、精确度：是近似数精确的程度，一般有两种形式：一是精确到哪一位；二是保留几个有效数字．
1、有理数乘法法则是重点，要准确而熟练地运用.
乘法运算时，先确定积的符号，特别是确定几个因式乘积的符号，然后再把各因式的绝对值相乘.带分数参与乘法运算时，要把带分数化成假分数.乘法的交换律、结合律、分配律在有理数的运算中应用非常广泛，对简便运算起很大作用要灵活运用.
2、有理数的除法，给出了两种形式的法则，用不同的法则计算，所得的商是相同的，但一般情况下，如果不能整除的，则选用“转化”的法则，即把除法转化为乘法来计算，能整除的就直接用除法法则计算较简便，熟练运用除法法则计算也是重点.
3、正确理解倒数的意义.
（1）乘积为1的两个数互为倒数；
（2）如果两个数互为倒数，那么它们符号相同，即正数的倒数是正数，负数的倒数是负数，0没有倒数.
（3）倒数等于本身的数是±1.
4、计算
例1、
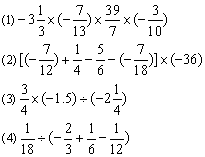
3、当近似数是小数形式时，它最后一位在什么位上，就说这个近似数精确到哪一位，对于带有记数单位的近似数，其精确度的确定，要先化为一般记法的数，再确定它的精确度．如8.03万等于80300，因为它是在十位上四舍五入的，所以它精确到百位，而不是百分位．
例5、某爆破人员执行爆破任务，点燃导火索后往100米外的安全地带奔跑，奔跑的速度为9米/秒，已知导火索燃烧的速度为每秒0.2米，导火索的长度应多长才能确保安全.（精确到0.1米）
解：100÷9×0.2=2.22…≈2.3（米）.
点评：此题不能用“四舍五入”法对2.22…取近似值2.2，因为2.2<2.22…，所以不能确保安全，所以应用“进一法”对2.22…取近似值2.3才能确保安全．因此在实际问题中不能一味用“四舍五入法”来取近似值，而应具体问题具体对待，正确选用“四舍五入法”、“进一法”和“去尾法”.
4、有理数的混合运算法则：先算乘方，再算乘除，最后算加减；如果有括号，先算括号里面的．
例6、计算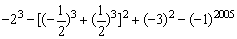
.
解：原式=－8－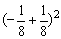
＋9＋1=－8＋9＋1=2.
点评：此题需注意－23=－8，(－3)2=9，(－1)2005=－1.
的值.
－cd的值.