我们之前所接触的都是数的运算，都是用已知数来表示数量关系，依据相等关系列出含未知数的等式则是方程，从算式到方程可以说是我们数学学习上的一个飞跃．
（一）、一元一次方程的有关概念
1、方程是含有未知数的等式；例如：
3x+5=8 ，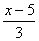 
= 
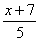，0.4y—2.5=0.1， 2x+3y=5
2、解方程就是求使方程中等号左右两边相等的未知数的值，这个值就是方程的解；
3、只含有一个未知数（元）x，未知数x的指数都是一（次）的方程叫一元一次方程；
例如： 3x+5=8，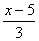 
= 
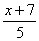，0.4y—2.5=0.1 是一元一次方程，而2x+3y=5则不是．
4、列方程时，要先设出未知数，然后根据问题中的相等关系，写出含有未知数的等式列出方程.
（二）、等式的性质
等式性质1：等式的两边都加（或减）同一个数（或式子），结果仍相等，
如果a＝b，那么a±c＝b±c；
等式的性质2：等式的两边乘同一个数，或除以同一个不为0的数，结果仍相等，
如果a＝b，那么ac＝bc；若c≠0，则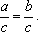
例1、下列式子中①x＞3；②3＋(－2)＝1；③m＝0；④－35x＋6x＝5；⑤x＋y＝0；⑥3x2＋2x哪些是方程.
分析：
含有未知数的等式叫方程，因此，要判断一个式子是不是方程，必须具备两个条件：一是等式，二是含有未知数 .
解：③④⑤是方程
①②⑥不是方程，因为①⑥不是等式，②是等式但不含有未知数
例2、2004年底，英才中学统计全校教师的学历情况，全校180名教师中，具有本科学历的有120名，比五年前增加了20%，那么五年前英才中学具有本科学历的教师有多少名？（只列方程，不必求解）
分析：
2004年度，英才中学具有本科学历的教师有120名，比五年前增加20%，因此2004年具有本科学历的教师人数，又是五年前具有本科学历的教师人数的(1＋20%)倍.
解：设五年前英才中学有 x名教师具有本科学历，
列方程得：
x(1＋20%)＝120
例3、根据下列问题，列出方程，不必求解.
（1）把若干本书发给学生，如果每人发4本，还剩下25本；如果每人发5本，还差5本，问学生有多少人？
（2）某班50名学生准备集体去看电影，电影票中有1.5元的和2元的，买电影票共花88元，问这两种电影票应各买几张？
分析：
（1）如果每人发4本，还剩下25本，即书数＝学生数×4＋25；如果每人发5本，还差5本，即书数＝ 学生数×5－5.
（2）共50名学生，因此共买50张共花88元，即两种票的钱数之和为88元.
解：（1）设学生x人，列方程：
4x＋25＝5x－5
（2）设买了1.5元的票x张，则2元的票买了(50－x)张.列方程：
1.5x＋2(50－x)＝88
例4、小明测量他家的客厅，长比宽多
，已知长为6米，宽多少米？（只列方程，不必求解）
错解一：设宽为 x米，列方程：
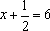
错解二：设宽为 x米，列方程：
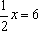
剖析：这里未弄清“增加
”的含义而出错.长比宽多的部分是宽的
.
正确解：设宽为 x米，列方程
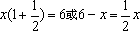
例5、根据等式的性质填空.
（1）已知a＝c，则2a－b＝________
（2）已知m＝n，则5＋m＝_________
分析：（1）比较两个等式左边的变化“a→2a－b”，是a的2倍减b，
因此右边应为c的2倍减b．
（2）m→5＋m，相当于等式的左边加5，因此右边也应该加5.
解： （1）因为a＝c，所以2a＝2c，所以2a－b＝2c－b；
（2）因为m＝n，所以5＋m＝5＋n.
例6、利用等式的性质解方程
（1）x＋5＝－2 （2）－2x－3＝25 （3）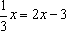
分析：
解方程就是求未知数 x的值，即写成“x＝？”的形式，因此,利用等式的性质，使等式左边的常数能抵消，必须加左边常数的相反数；右边的未知数能抵消，就要加右边未知数的相反数.
解：（1）方程两边都加－5（或都减去5）
x＋5－5＝－2－5
合并得：x＝－7
（2）方程两边都加3，得：
－2x－3＋3＝25＋3
合并得：－2x＝28
方程两边都除以－2（或两边都乘以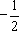
），得：
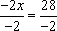
约分得：x＝－14
（3）方程两边都加－2x，得：
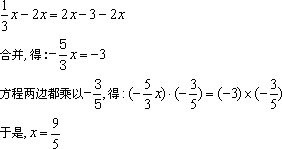
例7、判断下列变形是否正确
（1）若ac＝bc，则a＝b
（2）若a＋x＝b，则x＝a＋b
（3）若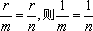
（4）若m(a2＋1)＝n(a2＋1)，则m＝n
分析：
初步看起来，好象都是正确的，但根据等式的性质不难发现，（ 1）中的变形是两边都除以了c，当c＝0时，显然不符合等式的性质2，是错误的；（2）中的变形，是要抵消左边的a，应两边都减去a，但右边却加上了a，也是错误的；想一想，（3）的变形过程符合等式的性质2吗？注意r＝0时呢？
由于a2是非负数，因为a2＋1是正数，（4）的变形过程是等式两边都除以
(a2＋1)，符合等式的性质2.
解：（1）× （2）× （3）× （4）√
