|
主讲: 高级教师 余国琴
一周强化
一、一周知识概述
1、角的平分线的作法
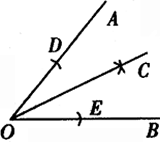
(1)在∠AOB的两边OA、OB上分别截取OD、OE,使OD=OE.
(2)分别以D、E为圆心,以大于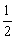 DE长为半径画弧,两弧交于∠AOB内一点C. DE长为半径画弧,两弧交于∠AOB内一点C.
(3)作射线OC,则OC为∠AOB的平分线(如图)
指出:(1)作角的平分线的依据是三角形全等的条件——“SSS”.
(2)角的平分线是一条射线,不能简单地叙述为连接.
2、角平分线的性质
在角的平分线上的点到角的两边的距离相等.
指出:(1)这里的距离是指点到角两边垂线段的长.
(2)该结论的证明是通过三角形全等得到的,它可以独立作为证明两条线段相等的依据.即不需再用老方法——全等三角形.
(3)使用该结论的前提条件是有角的平分线,关键是图中有“垂直”.
3、角平分线的判定
到角的两边的距离相等的点在角的平分线上.
指出:(1)此结论是角平分线的判定,它与角平分线的性质是互逆的.
(2)此结论的条件是指在角的内部有点满足到角的两边的距离相等,那么过角的顶点和该点的射线必平分这个角.
4、三角形的角平分线的性质
三角形的三条角平分线相交于一点,且这点到三角形三边的距离相等.
指出:(1)该结论的证明揭示了证明三线共点的证明思路:先设其中的两线交于一点,再证明该交点在第三线上.
(2)该结论多应用于几何作图,特别是涉及到实际问题的作图题.
二、重难点知识归纳
角平分线的画法、性质和判定,性质和判定的应用.
三、典型例题剖析
例1、如图,已知点C为直线AB上一点,过C作直线MN,使MN⊥AB.
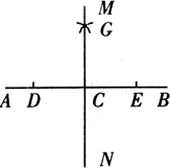
分析:由C点在AB上可知∠ACB=180°,要作MN⊥AB于C,即是作∠MCA=90°,因此可以作出平角∠ACB的平分线即可.
作法:(1)以C为圆心,以任意长为半径画弧交AB于D、E两点.
(2)分别以D、E为圆心,以大于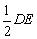 长为半径画弧,两弧交于点G. 长为半径画弧,两弧交于点G.
(3)过C、G作直线MN,则MN⊥AB.
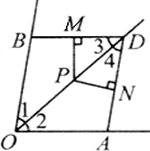
例2、如图所示,OD平分∠AOB,在OA、OB边上取OA=OB,PM⊥BD,PN⊥AD,求证:PM=PN.
分析:因为PM⊥BD,PN⊥AD,所以要证PM=PN,只需证∠3=∠4即可.而∠3=∠4可通过证△OBD≌△OAD得到.
证明:因为OD平分∠AOB,所以∠1=∠2(角平分线定义).
在△OBD和△OAD中,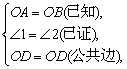
所以△OBD≌△OAD(SAS).
所以∠3=∠4(全等三角形的对应角相等).
又因为PM⊥BD,PN⊥AD(已知),
所以PM=PN(在角的平分线上的点到这个角的两边的距离相等).
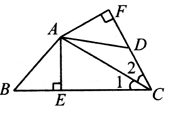
例3、已知:如图所示,在△ABC中,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,求证:AD⊥EF.
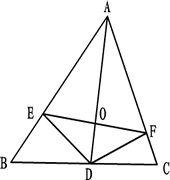
分析:欲证:AD⊥EF,就要证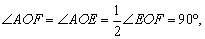
所以考虑证△AEO≌△AFO,由题中条件可知△AEO、△AFO已有一边(公共边)一角对应相等,要证AE=AF,问题就解决了,所以需先证明△AED≌△AFD.
证明:AD是∠BAC的平分线,DE⊥AB,DF⊥AC(已知),
所以DE=DF(角平分线上的点到这个角的两边距离相等).
在Rt△AED和Rt△AFD中,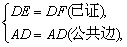
所以Rt△AED≌Rt△AFD(HL).
所以AE=AF(全等三角形对应边相等).
在△AEO和△AFO中,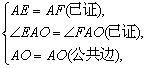
所以△AEO≌△AFO(SAS).
所以∠AOE=∠AOF(全等三角形对应角相等).
所以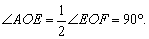 所以AD⊥EF(垂直定义). 所以AD⊥EF(垂直定义).
例4、如图所示,四边形ABCD中,AB=AD,AC平分∠BCD,AE⊥BC,AF⊥CD.求证:△ABE≌△ADF.
证明:因为AC平分∠BCD,AE⊥BC,AF⊥CD,
所以AE=AF(角平分线上的点到角的两边的距离相等).
在△ABE与△ADF中,AE=AF,AB=AD(已知),∠AEB=∠AFD=90°,
所以Rt△ABE≌Rt△ADF(HL).即△ABE≌△ADF.
例5、如图所示,BE、CF是△ABC的高,BE、CF相交于O,且OA平分∠BAC.求证:OB=OC.
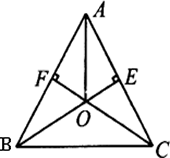
分析:要证OB=OC,需证△BOF≌△COE,条件有对顶角,直角,又OA是角平分线,不难证OF=OE,此问题得证.
证明:因为BE⊥AC,AB⊥CF(已知),
所以∠BFO=∠CEO=90°(垂直定义).
又因为BE、CF相交于O,且OA平分∠BAC,
所以OF=OE(角平分线上的点到角两边的距离相等).
在△BOF和△COE中,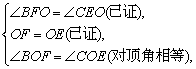
所以△BOF≌△COE(ASA),所以OB=OC(全等三角形的对应边相等).
例6、“角平分线上的点到角的两边距离相等,到角的两边的距离相等的点在角的平分线上”,如图所示:(1)若∠BAD=∠CAD,且BD⊥AB于B,DC⊥AC于C,则BD=CD,(2)若BD⊥AB于B,DC⊥AC于C,且BD=CD,则∠BAD=∠CAD.试利用上述知识,解决下面的问题:三条公路两两相交于A、B、C三点,现计划修建一个商品超市,要求这个超市到三条公路距离相等,问可供选择的地方有多少处?
你能在图中找出来吗?
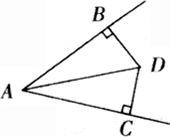
分析:解此题时受思维定势的影响,容易这样想:修建点到AB、BC、CA的距离相等,则该点就应是△ABC的三个内角的平分线的交点,其实在△ABC的外部也存在满足条件的点.
解:如图所示:
(1)作出△ABC两内角的平分线,其交点为O1;
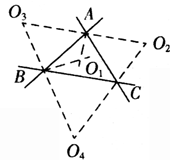
(2)分别作出△ABC两外角平分线,其交点分别为O2,O3,O4;
故满足条件的修建点有四处,即O1, O2,O3,O4.
- 返回 -
|