|
主讲: 中学高级教师 余国琴
一周强化
一、一周知识概述
勾股定理
如果直角三角形的两条直角边长分别为a、b,斜边为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.
指出:
(1)我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,即勾2+股2=弦2.
(2)勾股定理反映了直角三角形三边之间的数量关系,因此是直角三角形的性质定理,它为我们利用计算的方法研究几何图形的性质提供了新的途径.
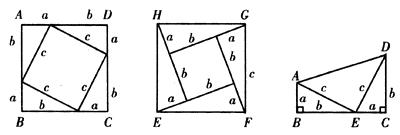
(3)勾股定理的证明常用面积法证明,读者可根据图的几种拼图方式,用面积证明勾股定理.
(4)勾股定理只适用于直角三角形,对于一般非直角三角形就不存在这种关系.勾股定理的作用是:①已知直角三角形的两边求第三边;②在直角三角形中,已知其中的一边,求另两边的关系;③用于证明平方关系;④利用勾股定理,作出长为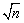 的线段. 的线段.
二、重点、难点、疑点突破
1、勾股定理
勾股定理在西方又被称为毕达哥拉斯定理,它有着悠久的历史,蕴涵着丰富的文化价值.勾股定理是数学史上的一个伟大的定理,在现实生活中有着广泛的应用,被人誉为“千古第一定理”.
勾股定理反映了直角三角形(三边分别为a,b,c,其中c为斜边)的三边关系,即c2=a2+b2.
它的变形为c2-a2=b2或c2-b2=a2.
运用它可以由直角三角形中的两条边长求第三边.
例如:已知一个直角三角形两边长分别为3cm,4cm,求第三边长.
因为该题设没有说明哪条边是直角三角形的斜边,所以要进行分类讨论.
当两直角边分别为3cm,4cm时,由勾股定理有斜边为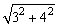 =5cm; =5cm;
当斜边为4cm,一直角边为3cm时,则另一直角边为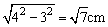 . .
故第三边为5cm或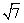 cm. cm.
2、直角三角形的几个性质
(1)两锐角互余;
(2)三边长满足勾股定理;
(3)如果有一个锐角等于30°,那么所对的直角边(设此边长为a)等于斜边的一半,三边长的关系为a,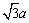 ,2a; ,2a;
(4)等腰直角三角形(直角边边长为a)三边长的关系为a,a,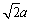 ; ;
(5)面积等于两直角边乘积的一半.
3、用尺规画长为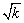 的线段 的线段
教材中介绍了用尺规画长为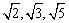 的线段的作法,对画长为 的线段的作法,对画长为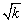 (k为自然数)的线段,我们通常可将k写成两个自然数的平方和或平方差来解决. (k为自然数)的线段,我们通常可将k写成两个自然数的平方和或平方差来解决.
例如用尺规画长为 的线段. 的线段.
因为21=25-4=52-22,所以画Rt△ABC,使一条直角边AC=2,斜边AB=5,则另一条直角边BC=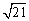 ; ;
同理,因为37=36+1=62+12,所以画Rt△ABC,使两直角边AC=1,BC=6,则斜边AB=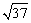 . .
4、数形结合思想
数形结合是中学数学中一种重要思想方法,它把代数的精确描述与几何图形的直观结合起来,从而使几何问题代数化,代数问题几何化,也将抽象思维与形象思维有机地结合在一起,实现了数与形的统一.正如华罗庚所说:“数缺形时少直觉,形缺数时难入微.”
例如对于勾股定理的证明,教材中就是以几何直观形式呈现的,清晰易懂.又由图,我们不难得出下面的结论:
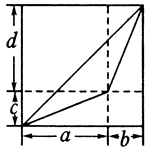
对于正数a,b,c,d,如果a+b=c+d,那么, . .
结合图形,如何证明,同学们不妨一试,亲身体验数形结合的神奇!
三、典型例题剖析
1、运用勾股定理求值
例1、如图,在△ABC中,CD⊥AB于D,若AB=5,CD=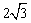 ,∠BCD=30°,求AC的长. ,∠BCD=30°,求AC的长.
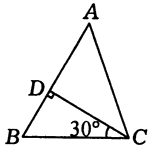
解:∵CD⊥AB于D,∠BCD=30°,∴BD=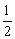 BC. BC.
设BD=x,则BC=2x.
在Rt△BCD中,由勾股定理有BD2+CD2=BC2,即
x2+(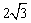 )2=(2x)2,解得x=2. )2=(2x)2,解得x=2.
∴BD=2,∵AB=5,∴AD=3.
在Rt△ACD中,由勾股定理有
AC2=AD2+CD2=32+(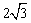 )2=21, )2=21,
∴AC=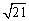 . .
点拨:
这里分别在两个直角三角形中运用了勾股定理,但含30°角的直角三角形的性质也给解题带来了很大的方便.
例2、如图,在△ABC中,∠A=90°,P是AC的中点,PD⊥BC于D,BC=9,DC=3,求AB的长.
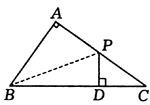
解:连结PB,BD=BC-DC=6.
在Rt△BDP和Rt△PDC中,
PD2=BP2-BD2,PD2=PC2-DC2,
∴BP2-BD2=PC2-DC2.
∴BP2- PC2=36-9=27.
∵AP=PC,∴BP2-AP2=AB2=27,
∴AB=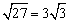 . .
点拨:
连结BP,在PD为公共边的两个直角三角形中运用勾股定理,得到BP2-PC2=BD2-DC2=27,是解答本题的关键所在.
例3、如图,在△ABC中,∠C=90°,AD、BE是中线,BE=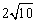 ,AD=5,求AB的长. ,AD=5,求AB的长.
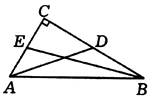
解:设CE=x,CD=y,则
AC=2x,BC=2y.
在Rt△ACD和Rt△BCE中,由勾股定理得
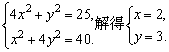
在Rt△ABC中,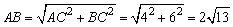 . .
点拨:运用勾股定理计算时,常设未知数,列方程或方程组来求解.
2、构造直角三角形解题
例4、如图,已知,∠A=60°,∠B=∠D=90°,AB=2,CD=1.求BC和AD的长.
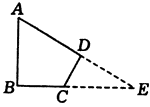
解:如图,延长BC,AD交于E.
∵∠B=90°,∠A=60°,
∴∠E=30°,∴AE=2AB=4.
同理CE=2CD=2.
在Rt△ABE中,BE2=AE2-AB2=16-4=12,
∴BE=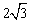 . .
在Rt△CDE中,DE2=CE2-CD2=4-1=3,
∴DE=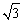 . .
∴BC=BE-CE=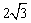 -2,AD=AE-DE=4- -2,AD=AE-DE=4-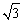 . .
点拨:
灵活根据图形及条件,构造直角三角形(其实也就是补图),创造条件去利用勾股定理解题.
例5、如图,在△ABC中,∠BAC=90°,AB=AC,点D、E在BC上,且∠DAE=45°,求证:CD2+BE2=DE2.
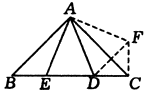
解:如图,将△ABE绕点A逆时针旋转90°得△ACF,则
∠ACF=∠B=45°,BE=CF,∠BAE=∠CAF.
又∵∠ACB=45°,∴∠DCF=90°.
∵∠EAD=45°,∴∠BAE+∠DAC=45°.
∴∠DAF=∠CAF+∠DAC=45°.
在△AED和△AFD中,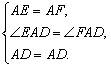
∴△AED≌△AFD,∴ED=FD.
又在Rt△CDF中,CD2+CF2=FD2,∴CD2+BE2=DE2.
点拨:
此题从待论证的结论可以联想到勾股定理,而三条线段不在同一个直角三角形中,故可运用旋转法将分散的线段集中在同一个三角形中.
3、运用面积法解题
例6、如图,△ABC中,∠B=90°,两直角边AB=7,BC=24.在三角形内有一点P到各边的距离相等,则这个距离是( )
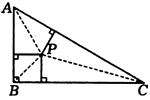
A.1 B.3
C.6 D.无法求出
解:依勾股定理知AC=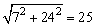 . .
设点P到各边的距离为r,连结PA、PB、PC.依三角形的面积关系,有
S△ABP+S△BCP+S△ACP=S△ABC,
即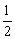 AB·r+ AB·r+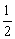 BC·r+ BC·r+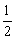 AC·r= AC·r=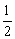 AB·BC. AB·BC.
得(7+24+25)r=7×24,解得r=3.
故选B.
点拨:
涉及到垂线段的问题,常可联系到某一三角形的高,从而可应用面积法来解题.因为它是一种代数方法,因此显得十分直观、简捷.
例7、如图,Rt△ABC的两直角边AB=4,AC=3,△ABC内有一点P,PD⊥BC于D,PE⊥AC于E,PF⊥AB于F,且 .求PD、PE、PF的长. .求PD、PE、PF的长.
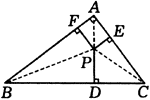
解:在Rt△ABC中,
∵AB=4,AC=3,∴BC=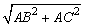 =5. =5.
设PF=x,PE=y,PD=z,则
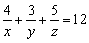 . ① . ①
连结PA、PB、PC.
∵S△PAB+S△PBC+S△PAC=S△ABC,
∴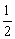 AB·x+ AB·x+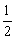 BC·z+ BC·z+ AC·y= AC·y=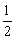 AB·AC, AB·AC,
即4x+3y+5z=12. ②
①+②,得4x+3y+5z+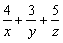 =24, =24,
配方,得
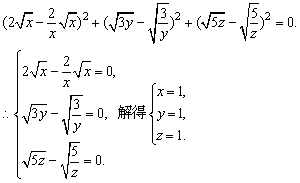
∴PD=PE=PF=1.
点拨:
本题显然不能直接运用勾股定理来计算PD、PE、PF的长,只能在连结PA、PB、PC后,将原三角形分成三个分别以AB、BC、CA为底,PF、PD、PE为高的三角形,由面积法列出关系式,再利用题设条件,即可求解.
4、构造几何图形解答代数问题
例8、设a、b、c、d都是正数,求证:
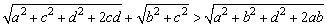 . .
分析:题中出现线段的平方和,考虑构造直角三角形,利用勾股定理证明.
证明:构造一个边长分别为(a+b)、(c+d)的矩形ABCD(如图).
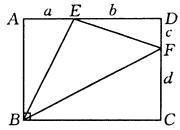
在Rt△ABE中,
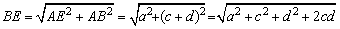 . .
在Rt△BCF中,
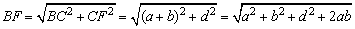 . .
在Rt△DEF中,
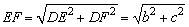 . .
在△BEF中,BE+EF>BF,即
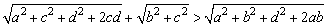
点拨:
勾股定理将直角三角形的位置关系(两边垂直)转化为数量关系,这为我们运用代数方法研究几何问题提供了工具,反过来,对有些代数问题,特别是含有平方和或平方差的代数式,我们也可以通过构造直角三角形用勾股定理来解决,即用几何方法解决代数问题.
- 返回 -
|