1、等差(比)数列的定义
如果一个数列从第二项起,每一项与它的前一项的差(比)等于同一个常数,这个数列就叫做等差(比)数列.
2、等差(比)数列的通项公式和前n项的公式
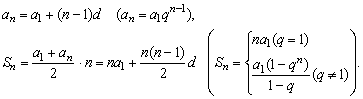
3、等差(比)中项的概念
如果在a与b中间插入一个数A,使a,A,b成等差(比)数列,那么A叫做a与b的等差(比)中项.
4、等差(比)数列的主要性质
(1)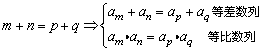 (m、n、p、q均为自然数).
(m、n、p、q均为自然数).
(2)在等差(比)数列{an}中,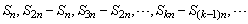 成等差(比)数列,其中Sn为前n项的和.
成等差(比)数列,其中Sn为前n项的和.
(3)在等差数列{an}中,an=am+(n-m)d,其中d为公差;在等比数列{an}中,an=amqn-m,其中q为公比.
1、分别用累加法求具有an+1=an+f(n)的数列的通项,
用累积法求具有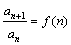 的数列的通项,
的数列的通项,
用拼凑分离法,求具有an+1=Aan+B(A、B为常数)的数列的通项.
2、数列{an}为等差数列的判定和证明
①证明方法:定义法即若一个数{an}满足an+1-an=d(d是一个与n无关的常数),则数列{an}为等差数列.
③常见的判定方法(充要条件):若一个数列{an}满足an=
an-1+d或Sn=an2+bn(d、b为常数)或2an+1=
an+an+2,则这个数列为等差数列.
3、数列{an}为等比数列的判定和证明
①定义法,若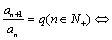 数列{an}为等比数列.
数列{an}为等比数列.
②等比中项法,若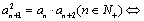 数列{an}为等比数列.
数列{an}为等比数列.
③通项法: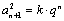 (k,q为非零常数,
(k,q为非零常数,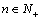 )
)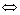 数列{an}为等比数列.
数列{an}为等比数列.
例1、已知下面各数列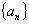 的前
的前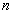 项和
项和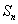 的公式,求
的公式,求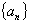 的通项公式。
的通项公式。
(1)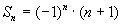 (2)
(2)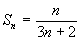
解:(1)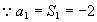 ,
,
当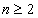 时,
时,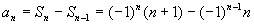
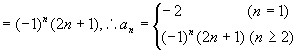
(2)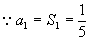 ,
,
当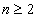 时,
时,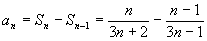
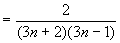 ,
,
由于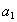 也适合于
也适合于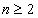 时的通项公式,
时的通项公式,
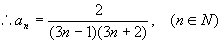 。
。
点评:
an与Sn的关系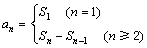 ,是一个非常重要的关系,根据这一关系,若知数列的前n项和Sn,则数列的通项an一定可求,但首项a1是否符合an=
Sn-Sn-1,需进一步验证,若不符合,则an需用分段函数表示,否则可合写为一个式子.(1)中的
,是一个非常重要的关系,根据这一关系,若知数列的前n项和Sn,则数列的通项an一定可求,但首项a1是否符合an=
Sn-Sn-1,需进一步验证,若不符合,则an需用分段函数表示,否则可合写为一个式子.(1)中的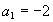 不适合
不适合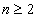 时的通项公式,故必须分类表达。
时的通项公式,故必须分类表达。
例2、若数列{an}是等差数列,数列{bn}满足bn=an·an+1·an+2(n∈N),{bn}的前n项和用Sn表示,若{an}中满足3a5=8a12>0,试问n多大时,Sn取得最大值?证明你的结论.
策略:
确定数列的单调性,利用不等式组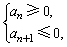 探讨{bn}中的项的正负关系是关键.
探讨{bn}中的项的正负关系是关键.
解答:∵ 3a5=8a12>0,∴ 3a5=(8a5+7d)
解得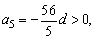
∴ d<0, ∴ 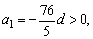
故{an}是首项为正数的递减数列.
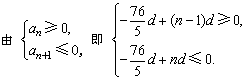
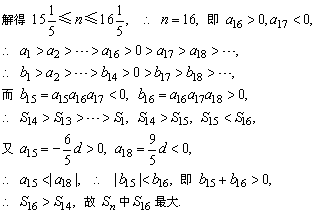
点评:
在等差数列中,求Sn的最大(小)值,其思路是找出某一项,使这项及它前面的项皆取正(负)值或零,而它后面的各项皆取负(正)值,则从第①项起到该项的各项的和为最大(小),即(1)当a1>0,d<0时,解不等式组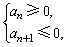 可得Sn达最大时的n值;(2)当an<0,d>0时,解不等式组
可得Sn达最大时的n值;(2)当an<0,d>0时,解不等式组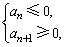 可得Sn达最小值的n值.
可得Sn达最小值的n值.
例3、一个等差数列的前12项和为354,前12项中偶数项和与奇数项和之比为32︰27,求公差d.
分析:
此题若选用前n项和公式建立方程组显然运算量大,而运用等差数列有关性质、采取整体思维的策略,则可大大简化计算过程.
解答:设前12项中偶数项与奇数项和为S偶、S奇,依题意得
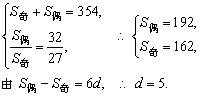
点评:在等差数列{an}中,
(1)项数为2n时,则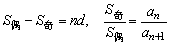 ;
;
(2)项数为2n-1时,则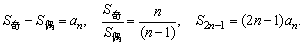
当{an}为等比数列时其结论可自己推导得出.
例4、设数列{an}和{bn}满足a1=b1=6, a2=b2=4, a3=b3=3,
且数列{an+1-an }(n∈N*)是等差数列,数列{bn-2}(n∈N*)是等比数列.
(Ⅰ)求数列{an}和{bn}的通项公式;
(II)是否存在k∈N*,使ak-bk∈(0,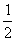 )?若存在,求出k;若不存在,说明理由.
)?若存在,求出k;若不存在,说明理由.
分析:
本题是一个探索性问题,解决此类问题的基本思路是假设存在,是否能求出符合条件的k值.
解答:(I)由已知a2-a1=-2, a3-a2=-1,
-1-(-2)=1,
∴an+1-an=(a2-a1)+(n-1)·1=n-3.
n≥2时,
an=( an-an-1)+( an-1-an-2)+…+( a3-a2)
+( a2-a1)+ a1
=(n-4)+(n-5) +…+(-1)+(-2)+6
=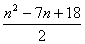 .
.
n=1也合适,∴an=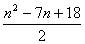 (n∈N*).
(n∈N*).
又b1-2=4、b2-2=2 .而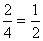
∴bn-2=(b1-2)·(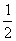 )n-1,即bn=2+8·(
)n-1,即bn=2+8·(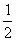 )n,
)n,
∴数列{an}、{bn}的通项公式为:an=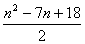 ,bn=2+(
,bn=2+(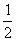 )n-3.
)n-3.
(II)设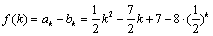
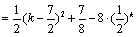
当k≥4时,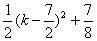 为k的增函数,-8·(
为k的增函数,-8·(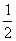 )k也为k的增函数,
)k也为k的增函数,
而f(4)= 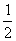 ,
,
∴当k≥4时,ak-bk≥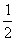 .
.
又f(1)=f(2)=f(3)=0 ,
∴不存在k,使f(k)∈(0,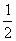 ).
).
点评:
(II)中想直接解不等式是现在无法解决的,但运用了函数的思想,使本题得以解决.数列与函数的综合是常考的题型,学会从其知识的交汇处寻找问题解决的突破口.